Question
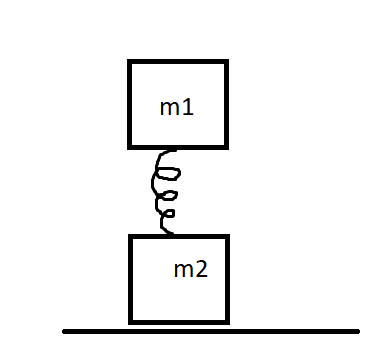
Question: The system when placed on a table as shown oscillates with frequency \[{f_1}\] . If the table is wit...
The system when placed on a table as shown oscillates with frequency f1 . If the table is withdrawn, the system oscillates with a frequency f2 . The ratio f22f12 will be:
(A) m1m1+m2
(B) m1+m2m2
(C) m1+m2m1
(D) None
Solution
Find the time period of oscillation of the system. Using time period, find the relation between time period and frequency for both objects individually. Divide the squares of frequency and find out the solution.
Complete step by step solution:
The figure given consists of 2 masses attached to a given spring of spring constant k and length x. When the table is withdrawn from the second mass, the system begins to have increased oscillations of frequency f2 . Now we can first find the time period required for the oscillations to occur.
This is mathematically expressed as ,
T=2π×km
Wherein T is the time period of oscillations, m is the mass of the object and K is the spring constant of the spring.
Now we know that frequency of an oscillation is inversely proportional to the time period of oscillations.
f=1/T
⇒f=1/(2π×km)
⇒f=2π1×mk
For Object 1,
⇒f1=2π1×m1k
For Object 2,
⇒f2=2π1×m2+m1k
Note: Since the table is removed, the frequency experienced by the downgoing object will also experience the mass of the first object .
Now f22f12 will be
⇒f2f1=2π1×m2+m1k2π1×m1k
Cancelling the like terms,
⇒f2f1=m2+m1km1k
Squaring on both sides we obtain,
⇒f22f12=m2+m1km1k
Removing spring constant k from the above equation,
⇒f22f12=m2+m11m11
⇒f22f12=m1m2+m1
Therefore, Option (A) is the correct answer to the following question.
Note:
The time period is defined as a time period required by a body expressing periodic motion to complete one period or one cycle. Frequency is defined as the repetition of the event per unit time. Frequency is measured in Hertz whereas the time period is measured in seconds. Frequency is inversely proportional to time period of the oscillation.
