Question

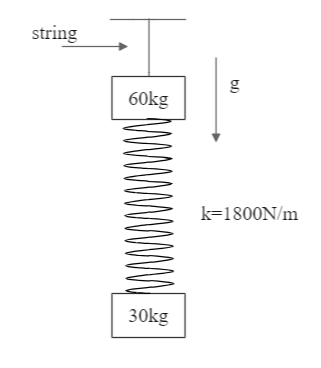
The system shown is hanging in equilibrium well above the ground. When the string is cut, the minimum time taken by the spring to reach its natural length after cutting is? (Take ${\pi ^2} = 10$)

(A) $\dfrac{1}{6}$ sec
(B) $\dfrac{1}{{12}}$ sec
(C) $\dfrac{1}{8}$ sec
(D) $\dfrac{2}{3}$ sec

Answer 1

For a system of masses to be in equilibrium, the forces acting on it need to be balanced. When a spring is present, it stretches or compresses as compared to its natural length to exert a force that helps balance the system.
Formula used: $T = 2\pi \sqrt {\dfrac{m}{k}}$, where T is the time period of oscillation of a simple-harmonic motion, m is the reduced mass of the system and k is the spring constant.

Complete step by step answer:
We are told that the provided system is in an equilibrium initially. When the string is cut off, the forces acting on the system will disperse and the spring will try to return to its original or natural length.
We have the following information about the system:
Mass $M = 60kg$
Mass $m = 30kg$
Spring constant $k = 1800N/m$
We know that a spring-mass system follows a simple harmonic motion with the time period given as:
$\Rightarrow T = 2\pi \sqrt {\dfrac{m}{k}}$
We calculate the reduced mass as:
$\Rightarrow \dfrac{{m \times M}}{{m + M}} = \dfrac{{30 \times 60}}{{30 + 60}} = \dfrac{{1800}}{{90}} = 20$kg
We substitute this value to get the time period as:
$\Rightarrow T = 2\pi \sqrt {\dfrac{{20}}{{1800}}} = 2\pi \sqrt {\dfrac{1}{{90}}}$
Solving it further, we get:
$\Rightarrow T = 2\pi \times \dfrac{1}{{3\sqrt {10} }} = 0.66$s
As this is the time period for a complete wave, the first intersection would occur at $t = \dfrac{T}{4}$
Hence, the minimum time taken to reach the length would be:
$\Rightarrow t = \dfrac{{0.66}}{4} = \dfrac{1}{6}s$
Hence, the correct answer is option (A).

Note:
The simple harmonic motion describes the restoring force on an object which is directly proportional to its displacement from the mean position. It is used to describe the motion of a spring because of the elastic restoring force that is exhibited by the spring. The SHM is sinusoidal in time and also demonstrates a single frequency.