Question

The system shown in the figure is in equilibrium. The blocks A, B and C are of equal masses, the inclined face is frictionless, the pulleys are light and frictionless, the thread is light and inextensible, the springs are light and the blocks B and C are connected to the axles of the respective pulleys by rigid links (g is acceleration due to gravity). Then

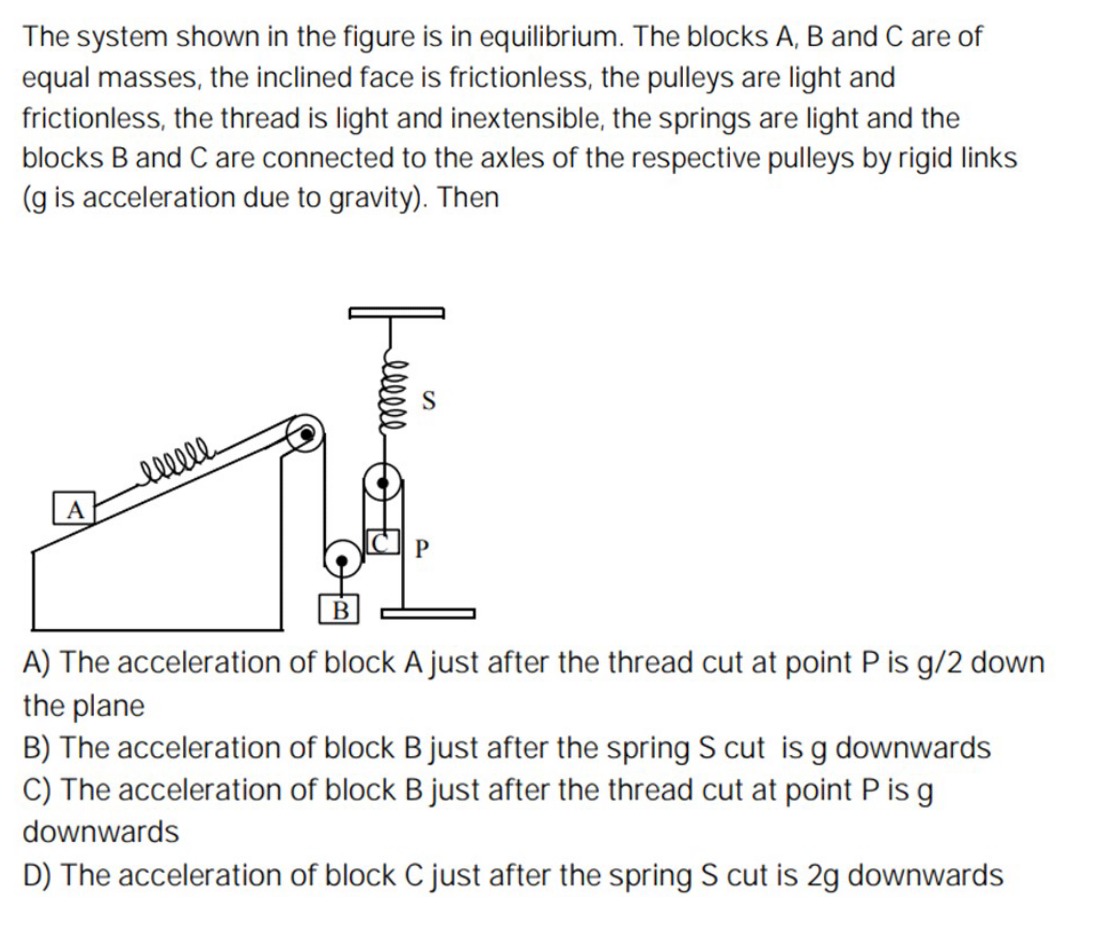
• A. The acceleration of block A just after the thread cut at point P is g/2 down the plane
• B. The acceleration of block B just after the spring S cut is g downwards
• C. The acceleration of block B just after the thread cut at point P is g downwards
• D. The acceleration of block C just after the spring S cut is 2g downwards

Answer 1

Answer: (A), (C)

The acceleration of block A just after the thread cut at point P is g/2 down the plane; The acceleration of block B just after the thread cut at point P is g downwards

Answer 2

Key idea: Immediately after a cut, tensions in the remaining segments of the light inextensible string do not change instantaneously.

1. After cutting at P: The fixed support on the RHS is removed, so the only support for the rope‐pulley system is the spring on the LHS. Block A (on a frictionless incline of angle θ with sinθ=½ at equilibrium) sees its weight component m g sinθ= m g/2 unbalanced, giving a= g/2 down the plane. Block B is attached to a massless pulley with equal tensions on both sides (still T= m g/2), so these cancel and the net vertical force is m g − 2T= m g − m g=0; however, the geometry of the string constrains B to fall at the same rate as A: its vertical acceleration resolves to g.
2. Other cuts: Cutting the spring S only removes the small tension support; the rope tensions on B remain unchanged initially, so it does not instantaneously accelerate at g, nor does C jump to 2g.
   Therefore, options A and C are correct.