Question
Question: The system shown in the figure is in equilibrium. The maximum value of \(W\) . So that the maximum v...
The system shown in the figure is in equilibrium. The maximum value of W . So that the maximum value of W . So that the maximum value of static frictional force on 100Kg body is 450N , will be:-
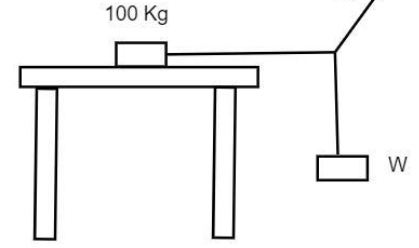
A) 100N
B) 250N
C) 450N
D) 1000N
Solution
The system is said to be equilibrium if all the force acts on the body is the same on all sides or else no force acts on the body. Draw the free body diagram of the given system of force. Equate the force acts on the body as from the free body diagram to find the weight of the body suspended.
Complete step by step solution:
It is given that the
Mass of the body, m=100Kg
Maximum value of the static frictional force, f=450N
Since the system is in equilibrium, all the force that acts on the system will be equal to each other. Let us draw the free body diagram from the given diagram.
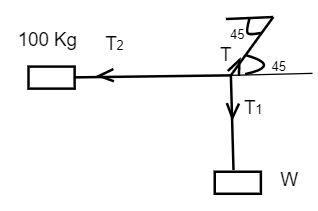
T1=T2=T
Splitting the force along the inclination into the horizontal component and the vertical component. That is Tsin45∘ and Tcos45∘ .
Substituting the known values in the above equation, we get
T1=W=Tsin45∘ …………………………(1)
T2=f=Tcos45∘ ………………………..(2)
We know that the value of the sin45∘ and the cos45∘ is 21 . Since the right hand side of both the equation (1) and (2) are equal, the left hand side must also be the same.
⇒W=f
Substituting the value of the maximum static frictional force in the above step, we get
⇒W=450N
Thus the option (C) is correct.
Note: Frictional force is the force offered by the surface against the movement of the body. In the above solution, the diagram shows that the 100Kg block is kept on a table. It stands on a certain place mainly due to the static friction it has. That so this force equates to its static friction.
