Question
Question: The system is shown in the figure and the man is pulling the rope from both sides with constant spee...
The system is shown in the figure and the man is pulling the rope from both sides with constant speed u. Then the speed of the block will be (M moves vertical)
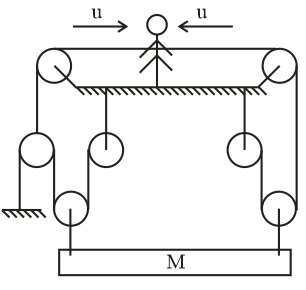
(A) 43u
(B) 23u
(C) 4u
(D) None of these
Solution
In a given problem, there are one block, and 7 pulleys in the system. So, first remember the concept of 2 block and one pulley system i.e.,
Velocity of pulley is the average velocity of string on both sides.
Now using the above concept, we will calculate the velocity of the block.
Complete step by step answer:
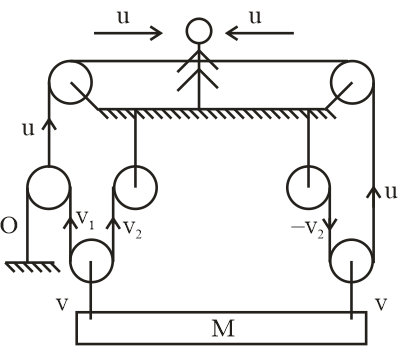
Here given that a man is pulling the rope from both sides with constant speed u.
We know that velocity of pulley is average of velocities of string on both sides.
So, from diagram
u=20+v1⇒u=2v1
v1=2u …..(1)
Now again from diagram
Velocity of block ⇒v=2v1+v2
2v=v1+v2 …..(2)
And from diagram we can also write
v=2u−v2
2v=u−v2 …..(3)
From equation 2 + 3
4v=v1+u …..(4)
From equation 1 and 4
4v=2u+u
⟹4v=3u
∴v=43u
So, the velocity of the block is 43 times of speed u.
So, the correct answer is “Option A”.
Note:
Alternatively, this problem also can be solved by tension division as
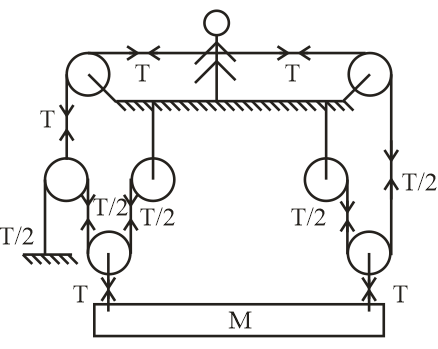
A man is pulling the rope from both sides with constant speed u.
According to the diagram.
Applying of virtual work method ΣT⋅V=0
Let the velocity of mass M be v in upward direction now,
−Tu−2uT+2Tv=0
⟹−22Tu−Tu=−2Tv
⟹2−3Tu=−2Tv
∴v=43u
Hence, the speed of the block will be 43u.
