Question

The system is released from rest. All the surfaces are smooth. Find the angle $\theta$ at which the acceleration of wedge is maximum. $\dfrac{M}{m}=\dfrac{1}{2}$

Answer 1

In this question we have been asked to calculate the inclination of the wedge or the angle $\theta$ for which the acceleration of the wedge will be maximum. To solve this question, we shall first calculate the acceleration of the wedge, in terms of $\theta$using a proper FBD. Later we shall determine the angle by substituting the maximum value of acceleration.

Complete step by step solution:
Since it is given that all the surfaces are smooth, when the block with mass m is released the wedge will move in the opposite direction due to sliding of the block of mass m. The free body diagram of the system when it is released from rest is as shown in the diagram below.

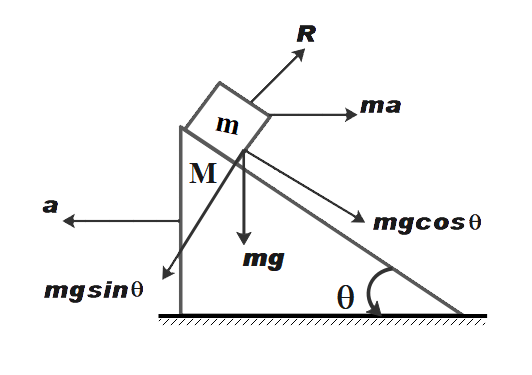
Now,
From the FBD,
The total acceleration with respect to wedge will say $a'$ be given by,
$a'=\cos \theta +g\sin \theta$
Now, we know that for maximum acceleration of the wedge,
$\dfrac{da'}{d\theta }=0$
Therefore, substituting the value ,We get,
$\dfrac{d\left( a\cos \theta +g\sin \theta \right)}{d\theta }=0$
On solving We get,
$\tan \theta =\dfrac{g}{a}$
Therefore,
$a=\dfrac{g}{\tan \theta }$
From the above equation, we can say that for the acceleration to be maximum, the value of $\tan \theta$ should be minimum.
We also know that,
$\tan 45{}^\circ =1$
Therefore, We can say that,
$\theta =45{}^\circ$
Therefore, the wedge will be at maximum acceleration when $\theta$ is 45 degrees.

Note:
The graphical representation used to visualize force, moments and reactions due to force on a body of certain mass is known as the Free Body Diagram or FBD. In this diagram every individual part of the system on which the force is applied or has a reaction to applied force is shown. It is also known as the force diagram.