Question
Question: The system is released from rest. 2 second after the release the heavier block is held for an instan...
The system is released from rest. 2 second after the release the heavier block is held for an instant and again released. Find the time elapsed after the momentary stopage of heavier block that the string again become tight.
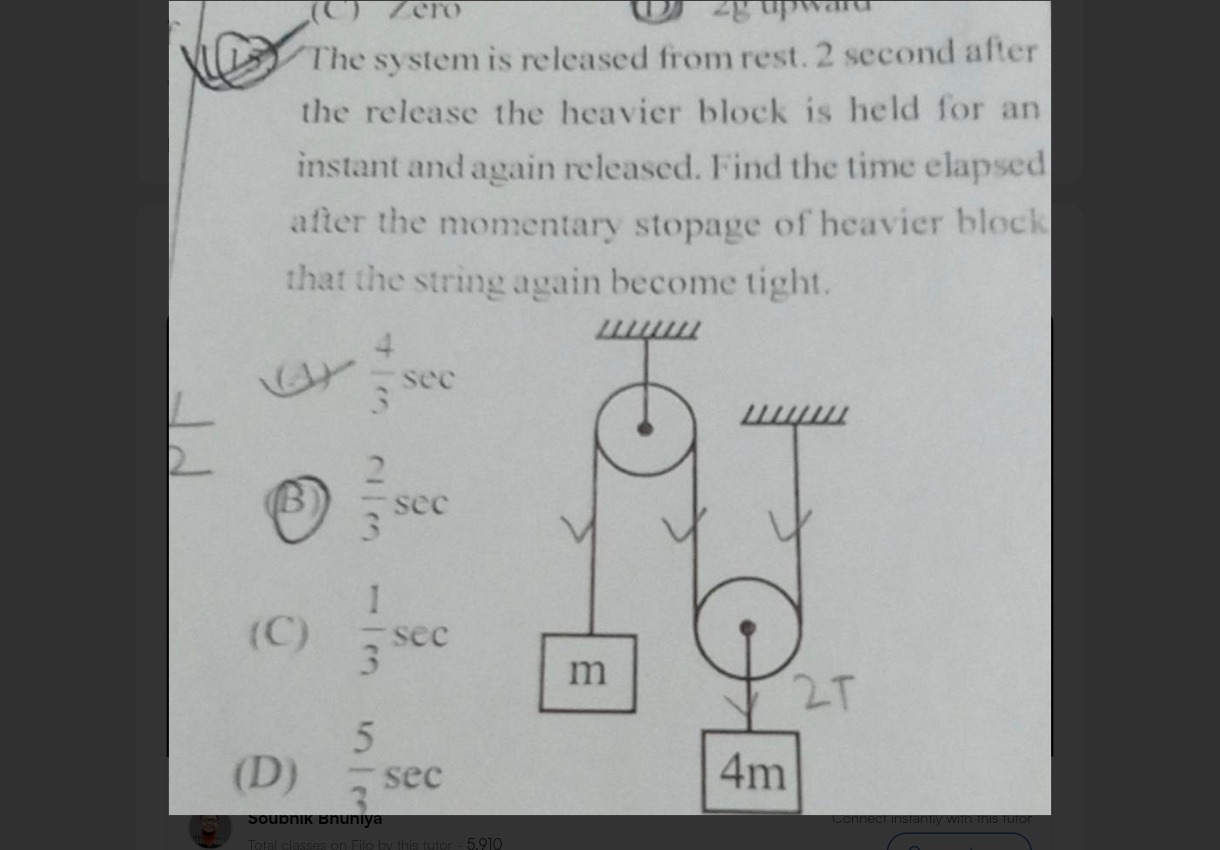
34 sec
32 sec
31 sec
35 sec
2/3 sec
Solution
The problem involves a system of blocks and pulleys. We need to analyze the motion in two phases:
- Initial motion until 2 seconds.
- Motion after the heavier block is momentarily stopped and released.
Phase 1: Initial motion (0 to 2 seconds)
Let am be the acceleration of mass 'm' and a4m be the acceleration of mass '4m'. Let 'T' be the tension in the string.
From the pulley configuration, the acceleration constraint is: If mass 'm' moves up by a distance x, the movable pulley (and thus mass '4m') moves down by x/2. So, if am is the upward acceleration of 'm', and a4m is the downward acceleration of '4m', then: am=2a4m
Now, apply Newton's second law: For mass 'm' (upward positive): T−mg=mam (Equation 1)
For mass '4m' (downward positive): The movable pulley is supported by two segments of the string, each having tension 'T'. So, the upward force on '4m' is 2T. 4mg−2T=4ma4m (Equation 2)
Substitute am=2a4m into Equation 1: T−mg=m(2a4m)⟹T=mg+2ma4m
Substitute this expression for T into Equation 2: 4mg−2(mg+2ma4m)=4ma4m 4mg−2mg−4ma4m=4ma4m 2mg=8ma4m a4m=8m2mg=4g (downwards)
Now find am: am=2a4m=2(4g)=2g (upwards)
After 2 seconds, the velocities of the blocks are: Initial velocity u=0 for both. vm=u+amt=0+(2g)(2)=g (upwards) v4m=u+a4mt=0+(4g)(2)=2g (downwards)
Phase 2: Motion after momentary stoppage
At t=2 seconds, the heavier block (4m) is held for an instant and released. This means its velocity instantaneously becomes zero. The string becomes slack because mass 'm' still has an upward velocity.
Let t′=0 be the instant the heavier block is released (which corresponds to t=2 seconds in the overall timeline). At t′=0: vm(0)=g (upwards) v4m(0)=0
Since the string is slack, both blocks move independently under gravity. For mass 'm': It moves upwards with initial velocity g and is acted upon by gravity (downwards). So, its acceleration is am′=−g (if upward is positive). The displacement of 'm' from its position at t′=0 is Δym. Let upward displacement be positive. Δym(t′)=vm(0)t′+21am′t′2=gt′−21gt′2
For mass '4m': It starts from rest and falls under gravity. So, its acceleration is a4m′=g (downwards). The displacement of '4m' from its position at t′=0 is Δy4m. Let downward displacement be positive. Δy4m(t′)=v4m(0)t′+21a4m′t′2=0+21gt′2=21gt′2
The string will become tight again when the relative positions of the blocks satisfy the length constraint of the string. Let's define the positions from a fixed reference point (e.g., the ceiling). Let ym be the position of mass 'm' (downwards positive). Let yP be the position of the movable pulley (downwards positive). The total length of the string L is constant: L=(yP−yfixed_support)+(yP−yfixed_pulley)+(ym−yfixed_pulley) L=2yP+ym−(yfixed_support+2yfixed_pulley) Since L, yfixed_support, and yfixed_pulley are constants, we have: 2yP+ym=constant Differentiating twice with respect to time: 2aP+am=0 (where aP is acceleration of pulley, am is acceleration of mass 'm', both positive downwards). Since aP=a4m, 2a4m+am=0. This is the constraint when the string is tight.
Let's use the displacements from their positions at t′=0. Let Δym be the displacement of 'm' (downward positive). Let Δy4m be the displacement of '4m' (downward positive). The constraint implies that the change in length of the string must be zero for the string to be taut. The total length of the string is L=2yP+ym−C. So, 2ΔyP+Δym=0 (where ΔyP is the displacement of the movable pulley, same as Δy4m). Thus, 2Δy4m+Δym=0 is the condition for the string to become tight again.
From our earlier calculations for motion during slack: Δym(t′)=−(gt′−21gt′2)=−gt′+21gt′2 (converted to downward positive displacement) Δy4m(t′)=21gt′2 (downward positive displacement)
Substitute these into the condition 2Δy4m+Δym=0: 2(21gt′2)+(−gt′+21gt′2)=0 gt′2−gt′+21gt′2=0 23gt′2−gt′=0 gt′(23t′−1)=0
This equation gives two solutions:
- t′=0: This corresponds to the instant the heavier block was stopped.
- 23t′−1=0⟹23t′=1⟹t′=32 sec.
This is the time elapsed after the momentary stoppage of the heavier block that the string again becomes tight.
