Question

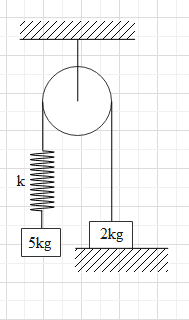
The system as shown in the figure is released from rest. The pulley, spring and the string are ideal and the friction is absent everywhere. If the speed of 5kg block when 2kg block leaves the contact with the ground is $2\sqrt{x}m{{s}^{-1}}$, then the value of x is (spring constant k=40N/m)

Answer 1

When the block leaves the ground the tension will be equal to the gravitational force acting on the 2kg block, i.e. T=2g. And tension is equal to the spring force ky. Hence, find the extension in the spring at the given instant. Then calculate the total work done on the 5kg block by gravity (W=mgy) and the spring force (${{W}_{s}}=-\dfrac{1}{2}k{{y}^{2}}$). Equate the total work done to the change in the kinetic energy of the block. Hence, find the speed of the block at the given instant. Then compare the speed with the given value and find the value of x.
Formula used:
${{F}_{s}}=ky$
${{W}_{s}}=-\dfrac{1}{2}k{{y}^{2}}$
W = mgy
$K=\dfrac{1}{2}m{{v}^{2}}$

Complete answer:
It is given that the speed of the block of mass 5kg when the block of 2kg leaves the contact with the ground is $2\sqrt{x}m{{s}^{-1}}$. Let this speed be equal to v.
Before the system is released, the 2kg block is at rest. Meaning the normal reaction of the ground balances the gravitational force i.e. equal to 2g (where g is the gravitational acceleration). As the system is released from rest, the tension in the string and the spring will begin to increase and the tension will act on the 2 kg block in upward direction.
Due to the tension (T), the spring will begin to stretch and exert a force on the 5kg block in upward direction. The spring force is given as ${{F}_{s}}=ky$, where k is the spring constant and y is the change in the length of the spring.

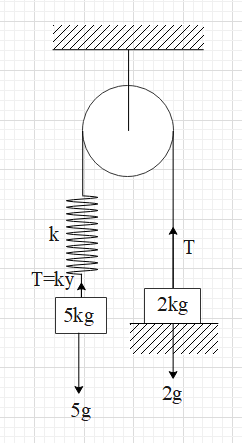
Therefore, there are two forces acting on the 5kg block - the gravitational force (5g) acting downwards and the spring force acting upwards (ky). Hence, both forces will do some work on the block, which will equal to the change in its kinetic energy.
Let us calculate the total work done on the block before the 2 kg block leaves the ground.
When the 2 kg block leaves the ground, the extension in the spring be y. And when this block leaves the ground, the tension will be equal to the gravitational force on the block.
i.e. T = 2g.
And T = ky.
This implies that ky = 2g …. (i).
The given value of k is 40N/m and let us consider the value of g as $10m{{s}^{-2}}$.
Substitute the values in equation (i).
$\Rightarrow (40)y=2\left( 10 \right)$
This means that the block is displaced by 0.5m.
Therefore, work done by the gravitational force on a 5kg block is W = mgy = $5(10)(0.5)=25J$.
The work done by a spring is given as ${{W}_{s}}=-\dfrac{1}{2}k{{y}^{2}}$.
${{W}_{s}}=-\dfrac{1}{2}(40){{(0.5)}^{2}}=-5J$
Therefore, the total work done is $W+{{W}_{s}}$.
The change in the kinetic energy of the block will be $\Delta K=\dfrac{1}{2}m{{v}^{2}}=\dfrac{5}{2}{{v}^{2}}$.
And $W+{{W}_{s}}=\Delta K$
$\Rightarrow 25-5=\dfrac{5}{2}{{v}^{2}}$
$\Rightarrow {{v}^{2}}=\dfrac{20\times 2}{5}=8$
$\Rightarrow v=2\sqrt{2}m{{s}^{-1}}$
This means that the speed of the block at the given instant is $v=2\sqrt{2}m{{s}^{-1}}$.
But $v=2\sqrt{x}m{{s}^{-1}}$
This means that x=2.

Note:
The sum of the potential energy of the spring and the kinetic energy of the body is called the mechanical energy of the spring block system.
The potential energy of the spring is given as $U=\dfrac{1}{2}k{{y}^{2}}$.
The kinetic energy of the body is $K=\dfrac{1}{2}m{{v}^{2}}$
The mechanical energy of the system is also to the work done by the external force, i.e. W=Fy.
Here, the external force is the gravitational force equal to 5g=50N.
This means, W=50y.
Therefore, W = K +U.
$50y=\dfrac{1}{2}m{{v}^{2}}+\dfrac{1}{2}k{{y}^{2}}$.
Here can substitute the value $y=0.5m$ and find the value of v.