Question

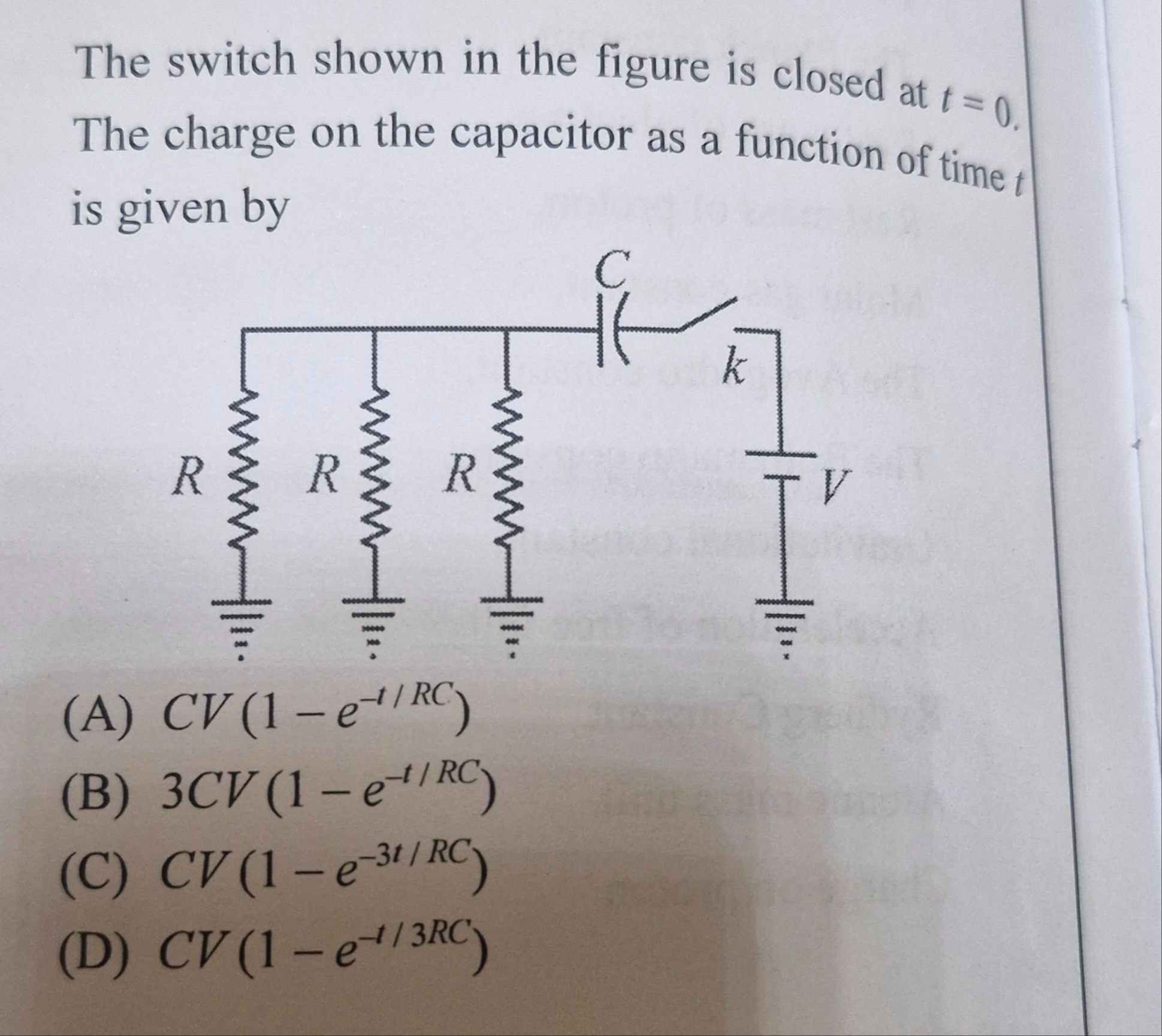
The switch shown in the figure is closed at $t=0$. The charge on the capacitor as a function of time t is given by

• A. CV(1-e^{-t/RC})
• B. 3CV(1-e^{-t/RC})
• C. CV(1-e^{-3t/RC})
• D. CV(1-e^{-t/3RC})

Answer 1

Answer: (C)

CV(1-e^{-3t/RC})

Answer 2

The circuit consists of a voltage source $V$ connected in series with a switch $k$, a capacitor $C$, and a parallel combination of three resistors, each with resistance $R$. When the switch is closed at $t=0$, the circuit becomes a series RC circuit.

1. Calculate the equivalent resistance: The three resistors $R$ are connected in parallel. The equivalent resistance $R_{eq}$ is given by: $\frac{1}{R_{eq}} = \frac{1}{R} + \frac{1}{R} + \frac{1}{R} = \frac{3}{R}$ $R_{eq} = \frac{R}{3}$

2. Determine the time constant: The time constant $\tau$ of an RC circuit is the product of the equivalent resistance and the capacitance: $\tau = R_{eq}C = \left(\frac{R}{3}\right)C = \frac{RC}{3}$

3. Determine the maximum charge: The maximum charge $Q_{max}$ on the capacitor when it is fully charged is given by $Q_{max} = CV_{source}$, where $V_{source}$ is the voltage of the source. In this case, $V_{source} = V$. $Q_{max} = CV$

4. Write the equation for charge as a function of time: For a capacitor charging in a series RC circuit, the charge $q(t)$ as a function of time is given by: $q(t) = Q_{max}(1 - e^{-t/\tau})$ Substituting the values of $Q_{max}$ and $\tau$: $q(t) = CV \left(1 - e^{-t/(RC/3)}\right)$ $q(t) = CV \left(1 - e^{-3t/RC}\right)$

Comparing this result with the given options, we find that it matches option (C).