Question

The switch is closed in the circuit shown. What is the charge on the capacitor when it is fully charged?

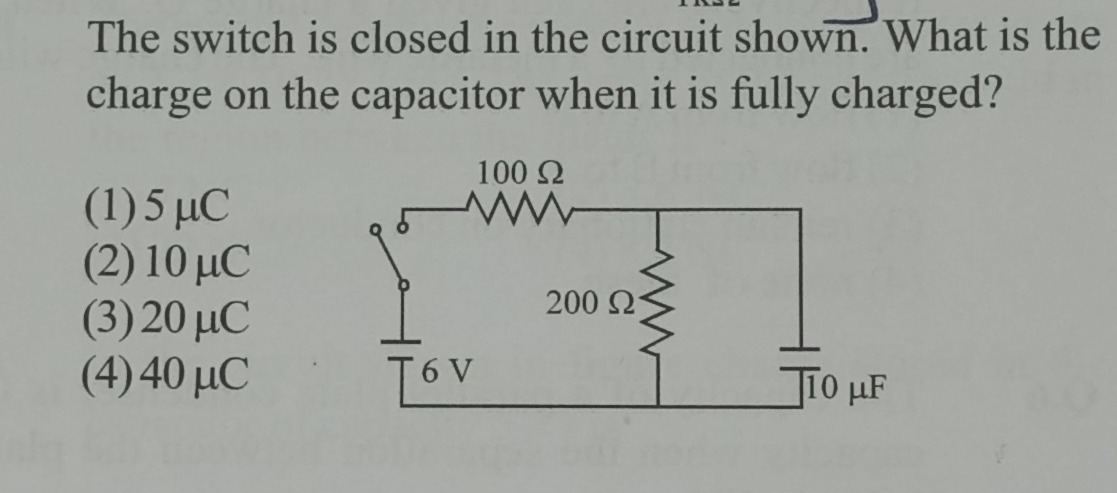
• A. 5 μC
• B. 10 μC
• C. 20 μC
• D. 40 μC

Answer 1

Answer: (D)

40 μC

Answer 2

When the switch is closed and the capacitor is fully charged, the circuit reaches a steady state. In the steady state, the current through the capacitor is zero, as a capacitor behaves like an open circuit in DC steady state.

In this circuit, the 10 $\mu$F capacitor is in parallel with the 200 $\Omega$ resistor. When the capacitor is fully charged, no current flows through the capacitor branch. The current from the 6V battery flows through the 100 $\Omega$ resistor and then through the 200 $\Omega$ resistor. Thus, the 100 $\Omega$ and 200 $\Omega$ resistors are effectively in series in the current path.

The total resistance in the circuit through which current flows is the sum of the resistances in series:

$R_{total} = R_1 + R_2 = 100 \, \Omega + 200 \, \Omega = 300 \, \Omega$.

The total voltage supplied by the battery is $V = 6 \, V$. The current flowing through the resistors in the steady state is given by Ohm's law:

$I = \frac{V}{R_{total}} = \frac{6 \, V}{300 \, \Omega} = 0.02 \, A$.

The voltage across the 200 $\Omega$ resistor is the product of the current flowing through it and its resistance:

$V_{200\Omega} = I \times R_2 = 0.02 \, A \times 200 \, \Omega = 4 \, V$.

Since the capacitor is connected in parallel with the 200 $\Omega$ resistor, the voltage across the capacitor when it is fully charged is equal to the voltage across the 200 $\Omega$ resistor:

$V_C = V_{200\Omega} = 4 \, V$.

The charge on the capacitor is given by the formula $Q = C \times V_C$, where $C$ is the capacitance and $V_C$ is the voltage across the capacitor. The capacitance is given as $C = 10 \, \mu F = 10 \times 10^{-6} \, F$. The voltage across the capacitor is $V_C = 4 \, V$.

Therefore, the charge on the capacitor when it is fully charged is:

$Q = C \times V_C = (10 \times 10^{-6} \, F) \times (4 \, V) = 40 \times 10^{-6} \, C = 40 \, \mu C$.