Question

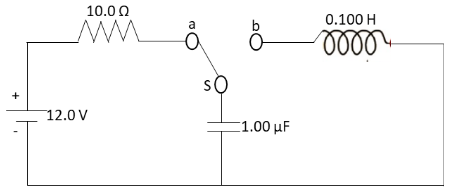
The switch in the figure is connected to a position for a long time interval. At $t = 0$ the switch is thrown to a position b. After this time

A. The frequency of oscillation of the LC circuit is $200\,{\text{Hz}}$
B. The maximum charge that appears on the capacitor is $12\,\mu {\text{C}}$
C. The maximum current in the inductor is $38\,{\text{mA}}$
D. The total energy the circuit possesses at $t{\text{ = 3}}{\text{.00}}\,{\text{s}}$ is $72\,\mu {\text{J}}$

Answer 1

We can use the formula for the frequency of oscillation in terms of capacitance and inductance and calculate the frequency of oscillation. We can also use the formula for the charge on the plates of the capacitor in terms of capacitance and potential difference. We can also use the law of conservation of energy and using the formulae for energy stored in capacitor and inductor, calculate the value of maximum current in the inductor and energy in the circuit.

Formulae used:
The frequency $f$ of oscillation is given by
$f = \dfrac{1}{{2\pi \sqrt {LC} }}$ …… (1)
Here, $L$ is the inductance and $C$ is the capacitance.
The charge $Q$ stored on the plates of the capacitor is
$Q = CV$ …… (2)
Here, $C$ is the capacitance and $V$ is the potential difference across the plates of the capacitor.
The maximum energy $U$ stored in the capacitor is
$U = \dfrac{1}{2}C{V^2}$ …… (3)
Here, $C$ is the capacitance and $V$ is the potential difference across the plates of the capacitor.
The maximum energy $E$ stored in the inductor is
$E = \dfrac{1}{2}LI_{\max }^2$ …… (4)
Here, $L$ is the inductance and ${I_{\max }}$ is the maximum current.

Complete step by step answer:
From the given circuit diagram, we can observe that the resistance of the resistor is $10.0\,\Omega$, capacitance of the capacitor is $1.00\,\mu {\text{F}}$ and inductance of inductor is $0.100\,{\text{H}}$.
$R = 10.0\,\Omega$
$\Rightarrow C = 1.00\,\mu {\text{F}}$
$\Rightarrow L = 0.100\,{\text{H}}$
The potential difference across the circuit is $12.0\,{\text{V}}$.
$V = 12.0\,{\text{V}}$
Let us first calculate the frequency of oscillation.Substitute $3.14$ for $\pi$, $0.100\,{\text{H}}$ for $L$ and $1.00\,\mu {\text{F}}$ for $C$ in equation (1).
$f = \dfrac{1}{{2\left( {3.14} \right)\sqrt {\left( {0.100\,{\text{H}}} \right)\left( {1.00\,\mu {\text{F}}} \right)} }}$
$\Rightarrow f = \dfrac{1}{{2\left( {3.14} \right)\sqrt {\left( {0.100\,{\text{H}}} \right)\left( {1.00 \times {{10}^{ - 6}}\,{\text{F}}} \right)} }}$
$\Rightarrow f = 503\,{\text{Hz}}$
Therefore, the frequency of oscillation is $503\,{\text{Hz}}$.Hence, the option A is incorrect.

Let now calculate the maximum charge stored on the plates of the capacitor.Substitute $1.00\,\mu {\text{F}}$ for $C$ and $12.0\,{\text{V}}$ for $V$ in equation (2).
$Q = \left( {1.00\,\mu {\text{F}}} \right)\left( {12.0\,{\text{V}}} \right)$
$\Rightarrow Q = 12.0\,\mu {\text{C}}$
Therefore, the maximum charge stored on the plates of the capacitor is $12.0\,\mu {\text{C}}$.Hence, the option B is correct.

According to the law of conservation of energy, the maximum energy stored in the capacitor is equal to the maximum energy stored in the inductor.
$U = E$
$\Rightarrow \dfrac{1}{2}C{V^2} = \dfrac{1}{2}LI_{\max }^2$
$\Rightarrow {I_{\max }} = \sqrt {\dfrac{C}{L}} V$
Substitute $1.00\,\mu {\text{F}}$ for $C$, $0.100\,{\text{H}}$ for $L$ and $12.0\,{\text{V}}$ for $V$ in the above equation.
$\Rightarrow {I_{\max }} = \sqrt {\dfrac{{1.00\,\mu {\text{F}}}}{{0.100\,{\text{H}}}}} \left( {12.0\,{\text{V}}} \right)$
$\Rightarrow {I_{\max }} = \sqrt {\dfrac{{1.00 \times {{10}^{ - 6}}\,{\text{F}}}}{{0.100\,{\text{H}}}}} \left( {12.0\,{\text{V}}} \right)$
$\Rightarrow {I_{\max }} = 0.0379\,{\text{A}}$
$\Rightarrow {I_{\max }} = 37.9\,{\text{mA}}$
$\Rightarrow {I_{\max }} = 38\,{\text{mA}}$
Therefore, the maximum current in the inductor is $38\,{\text{mA}}$.Hence, the option C is correct. The energy in the circuit remains conserved all the time. Hence, the energy in the circuit at any time is
$U = \dfrac{1}{2}C{V^2}$
Substitute $1.00\,\mu {\text{F}}$ for $C$ and $12.0\,{\text{V}}$ for $V$ in the above equation.
$U = \dfrac{1}{2}\left( {1.00\,\mu {\text{F}}} \right){\left( {12.0\,{\text{V}}} \right)^2}$
$\therefore U = 72\,\mu {\text{J}}$
Therefore, the energy in the circuit at any time is $72\,\mu {\text{J}}$. Hence, the option D is correct.

Hence, the correct options are B, C and D.

Note: The students should keep in mind that the energy is conserved in the circuit also. Hence, the energy stored in each component of the circuit should be conserved. Hence, there is no need to calculate the energy of the circuit at any particular time. The energy of the circuit remains the same all the time.