Question
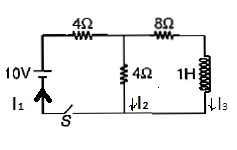
Question: The switch in figure is open for t < 0 then closed at time t = 0. Find the current in the inductor. ...
The switch in figure is open for t < 0 then closed at time t = 0. Find the current in the inductor.
A) i=7.5−0.25e−7t
B) i=1.5−0.25e−10t
C) i=1.5−0.25e−9t
D) i=1.5−0.25 e−12t
Solution
We are going to find out the value of current at time zero and at time infinity. At the time of zero there will be infinite resistance and at time infinity the inductor will be charged. Through net R(resistance) we will get the inductor current and after simplifying it we get our solution.
Complete step by step answer:
Step 1:
An inductor is a passive electronic component that stores energy in the form of a magnetic field. In its simplest form, an inductor consists of a wire loop or coil. The inductance is directly proportional to the number of turns in the coil. Inductance also depends on the radius of the coil and on the type of material around which the coil is wound.
At (t=0), we can see that no charge is going through the inductor so it will offer infinite resistance.
Then initially our current i1 =810 which is equal to 1.25A (∴V=iR) V is volt, I is current and R is resistance along inductor
Then at t=∞ (for a long time) inductor will be charged fully
Net resistance R equal to 4+8+48×4 which is equal to 320
i2 Will be equal to 32010 and this will give i2 equal to 1.5A
So along 8Ω there will be 0.5A current and along 4Ω there is 1.0A of current
Step 2:
Now we know that in the branch of inductor in saturation there is a 0.5A of current and it can be calculated as iL =0.51−eτt ……. (1) and here τL =RNETL (RNET is calculated across the branches of inductor)
RNET =10Ω and from here we will get value of τL=0.1sec
Now, equation (1) will have a form of iL =0.51−e0.1t which is equal to iL =0.5(1−e−10t)
Then i=1.25+0.251−e0.1t or it is equal to 1.5−0.25(1−e−10t)
Hence option B is correct
Note: In simple words we can say- use Ohm's Law and find the value of the total current: I = RV amp. Calculate the voltages across resistor R and inductor L by using Ohm's Law. If series inductors: Just add up the value of each individual inductor. Two or more identical parallel inductors: Add them up and divide by the number of inductors.
