Solveeit Logo
Login

Question

Question: The switch in figure is closed on \(a\) at time\(t=0.\) What is the ratio of \(\dfrac{\delta _l}{\...

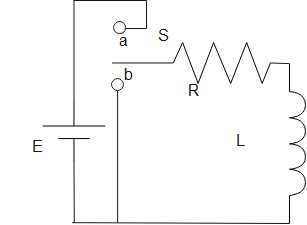
The switch in figure is closed on aa at timet=0.t=0.
What is the ratio of δlδ\dfrac{\delta _l}{\delta} of the inductors self-induced emf to the battery’s emf a) just after t=0t=0, b) at t=2.00τlt=2.00\tau_l, c) at what multiple ofτl\tau_l will δlδ=0.5\dfrac{\delta _l}{\delta}=0.5?

Explanation

Solution

We know that flow of current through a conductor varies the magnetic field around the conductor, the ability of the conductor to resist the change in magnetic field around it is called inductance. There are two types of inductances which are observed, namely the self-inductance and the mutual inductance.

Formula used:
E−EL=IRE-E_L=IR
EL(t)=Ee−tτLE_L(t)=Ee^{\dfrac{-t}{\tau_L}}

Complete step-by-step solution:
Inductance is defined as the effect of varying magnetic field to produce a current through the circuit as given here. Inductance is often measured in terms of henry. From the faraday’s law we know that this inductance is an opposing force, since inductance also produces an emf ELE_LThe phenomena of production of induced emf in the circuit when the current through it changes is called the self-induction, and also referred to as the back emf as it oppose the emf of the battery.
Thus, we can say that the total emf EE in the circuit is E=EL+IRE=E_L+IR
Self-inductance is also given as EL(t)=Ee−tτLE_L(t)=Ee^{\dfrac{-t}{\tau_L}}, since it varies with time.
Now consider the above given image,
a. When the switch is closed, we have E−EL=IRE-E_L=IR, since I=0I=0 at T=0T=0, we get EL=EE_L=E or ELE=1.0\dfrac{E_L}{E}=1.0
b. we know that EL(t)=Ee−tτLE_L(t)=Ee^{\dfrac{-t}{\tau_L}}, then the ELE_L at t=2.00τlt=2.00\tau_l will be
  ⟹  EL(t)=Ee−2τLτL=Ee−2\implies E_L(t)=Ee^{\dfrac{-2\tau_L}{\tau_L}}=Ee^{-2}
  ⟹  ELE=Ee−2E=0.135\implies \dfrac{E_L}{E}=\dfrac{Ee^{-2}}{E}=0.135
c. given, ELE=0.5\dfrac{E _L}{E}=0.5, then τl\tau_l will be
on rearranging we get,
  ⟹  tτl=ln(EEL)\implies \dfrac{t}{\tau_l}=ln\left(\dfrac{E}{E_L}\right)
  ⟹  tτl=ln2\implies \dfrac{t}{\tau_l}=ln 2
  ⟹  t=τLln2=0.693τL\implies t=\tau_L ln 2=0.693\tau_L
∴τL=t0.693\therefore \tau_L=\dfrac{t}{0.693}

Note: Also mutual induction occurs when two coils are coupled, namely the primary and the secondary coil. The primary coil creates a varying magnetic flux due to the passage of AC current, which in turn induces an EMF on the secondary coil. This is observed in the transformers.