Question

The surface area of the solid of revolution of the region bounded by y = 2x, x =0 and x = 2 about x-axis is,
a. $8\sqrt{5}\pi$
b. $2\sqrt{5}\pi$
c. $\sqrt{5}\pi$
d. $4\sqrt{5}\pi$

Answer 1

Hint: Draw the rough figure according to the boundaries which we get a triangle. Imagine the solid formed by revolving the base of the triangle. Find the surface area of the solid formed.

Complete step-by-step answer:
Given us three equations, y = 2x, x = 0 and x = 2. Now let us mark these points in a Cartesian plane.
Given, y = 2x.
By substituting x = 0, we get y = 0.
If x =2, we get, $y=2\times 2=4$.
Thus we have three points (0, 0), (2, 4) and (2, 0).

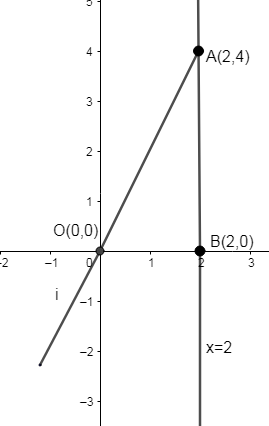
$\because$ x = 2 where y = 0 thus forms point (2, 0).
Let us take (2, 4), as coordinates of A.

Similarly, we can say that B (2, 0) and O (0, 0).

Now this figure we got $\vartriangle AOB$ becomes a right angled isosceles triangle, which is right angled at B.

The base of the triangle is 2 units along the x-axis and 4 units perpendicular to the x-axis.

A surface of revolution is a surface in Euclidean space created by rotating a curve around an axis of rotation.

The example of surfaces of revolution generated by the straight line are cylindrical and conical surfaces. A circle rotated around any diameter sphere.

Now if we rotate the triangle AOB about its base BO, then we may get a cone centered at B. So the base radius will be SB = 2 units, radius is represented as r. Thus, r = 4 units.

Similarly, height h = 2 units.

Therefore we need to find the curved surface area of the cone formed by surface revolution of triangle AOB.

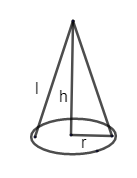
From the figure, l is the slant height.
We know, in a cone, ${{l}^{2}}={{r}^{2}}+{{h}^{2}}$
$\therefore l=\sqrt{{{r}^{2}}+{{h}^{2}}}$

The curved surface area of cone, $S=\pi rl$
$S=\pi r\sqrt{{{r}^{2}}+{{h}^{2}}}$

Substitute $l=\sqrt{{{r}^{2}}+{{h}^{2}}}$ in the surface area of a cone.
$\therefore S=\pi r\sqrt{{{r}^{2}}+{{h}^{2}}}$

And here, S = surface area of cone. Put r = 4 units, h =2 units.

& S=\pi \left( 2 \right)\sqrt{{{2}^{2}}+{{4}^{2}}} \\\ & S=2\pi \sqrt{4+16}=2\pi \sqrt{20} \\\ & S=2\pi \sqrt{2\times 10}=2\pi \sqrt{2\times 2\times 5} \\\ \end{aligned}$$ $$S=4\pi \sqrt{5}$$ Sq. unit. $$\therefore $$ The curved surface area of the cone = $$4\pi \sqrt{5}$$ Sq. unit. Thus option (d) is the correct answer. Note: In the question it's not mentioned to find the curved surface area of a cone. We need to find the solid formed from the rotation of the base of a triangle. Imagine the triangle rotating about its base and form the solid.