Question

The supply voltage to a room is 120V. The resistance of the lead wires is $6\Omega$ and a 60W bulb is already switched on. What is the decrease of voltage across the bulb, when a 240W heater is switched on in parallel to the bulb?
A. zero
B. $2.9{\text{ V}}$
C. $13.3{\text{ V}}$
D. $10.04{\text{ V}}$

Answer 1

Hint
As voltage depends on current and resistance, the addition of any component causes it to change. It is calculated by subtracting the final voltage from the initial voltage across the component in the circuit.
$\Rightarrow P = VI$ where $P$ is the power generated, $V$ is the voltage and $I$ is the current passing through the object in consideration.

Complete step by step answer
According to the question, we have an electrical setup that draws a certain potential from the constant supply. Then, a different electrical component is added into the circuit and we have to compute the voltage drop this leads to.
We are provided with the following data:
Supply voltage $V = 120{\text{ V}}$
Resistance of wire $R = 6{\text{ }}\Omega$
Bulb with wattage ${P_b} = 60{\text{ W}}$
Heater in parallel with the bulb ${P_h} = 240{\text{ W}}$
To better understand the setup, have a look at the following figure:

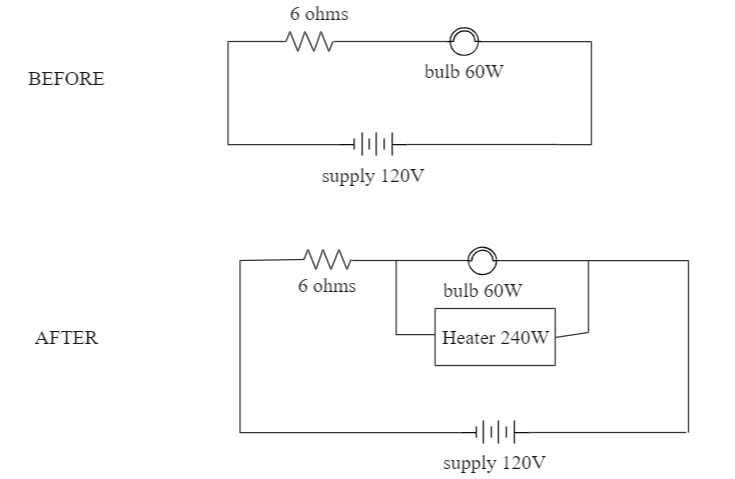
We first try to find the resistance of the bulb and the heater using the power law equation:
$\Rightarrow P = VI = \dfrac{{{V^2}}}{R}$ $[\because I = \dfrac{V}{R}]$
This can also be written as:
$\Rightarrow R = \dfrac{{{V^2}}}{P}$
Putting the values of R and solving for the bulb, we get:
$\Rightarrow {R_{bulb}} = \dfrac{{{{120}^2}}}{{60}}$
$\Rightarrow {R_{bulb}} = 240\Omega$
Similarly, calculating the resistance for heater, we get:
$\Rightarrow {R_{heater}} = \dfrac{{{{120}^2}}}{{240}}$
$\Rightarrow {R_{heater}} = 60\Omega$
Now, we will calculate the current across the bulb, in order to get the potential difference. Since, there are two resistances connected in series, we get the total resistance as:
$\Rightarrow {R_t} = R + {R_{bulb}}$
$\Rightarrow {R_t} = 6 + 240$
This gives us ${R_t} = 246\Omega$
Hence, current through the wire will be given by:
$\Rightarrow I = \dfrac{V}{{{R_t}}}$
Putting the values and solving for I, we have:
$\Rightarrow I = \dfrac{{120}}{{246}}A$
Using this current value, we find the voltage across the bulb:
$\Rightarrow {V_1} = I \times {R_{bulb}}$
$\Rightarrow {V_1} = \dfrac{{120 \times 240}}{{246}}$
On calculation, we have ${V_1} = 117V$ .
Moving on to the ‘after’ arrangement of circuit, we calculate the total resistance in parallel as this is what affects the voltage. We know that two resistances in parallel are calculated as:
$\Rightarrow {R_p} = \dfrac{{{R_1} \times {R_2}}}{{{R_1} + {R_2}}}$
Putting the values for ${R_{heater}}$ and ${R_{bulb}}$ gives us:
$\Rightarrow {R_p} = \dfrac{{60 \times 240}}{{60 + 240}}$
$\Rightarrow {R_p} = \dfrac{{60 \times 240}}{{300}}$
Further solving for the fractions, we get ${R_p} = 48\Omega$ .
We know that the voltage across the parallel arrangement is the same for all components.
So, we calculate the new current that flows across the parallel circuit:
$\Rightarrow I = \dfrac{{120}}{{{R_p} + R}}$
This will give us the voltage when the heater is connected as:
$\Rightarrow {V_2} = I \times {R_p}$
Putting the respective values we get,
$\Rightarrow {V_2} = \dfrac{{120}}{{48 + 6}} \times 48$
$\Rightarrow {V_2} = \dfrac{{5760}}{{54}}$
Hence, potential difference across the parallel arrangement is ${V_2} = 106.66V$
The voltage drop, when the heater is connected, will be the difference of ${V_1}$ and ${V_2}$ i.e.,
$\Rightarrow {V_1} - {V_2} = 117 - 106.66 = 10.34$
Upon subtraction, we get the voltage drop as $10.34V$ . This is approximately equal to $10.04V$ .
Hence, the answer is option (D) i.e. $10.04V$

Note
One important concept to remember while solving circuits in series and/or parallel is how the voltage and current are distributed in the two. In a series circuit, the voltage across each component is different and depends on the resistance, while the current remains the same. But in a parallel network, the current seems to change with the components and the voltage remains constant.