Question
Question: The sum of two point charges is\[7\mu C\]. They repel each other with a force of 1N when kept 30cm a...
The sum of two point charges is7μC. They repel each other with a force of 1N when kept 30cm apart in free space. Calculate the value of each charge.
& \text{A}\text{. 2}\mu C\text{ and 4}\mu C \\\ & \text{B}\text{. 2}\mu C\text{ and 5}\mu C \\\ & \text{C}\text{. 9}\mu C\text{ and 5}\mu C \\\ & \text{D}\text{. 4}\mu C\text{ and 7}\mu C \\\ \end{aligned}$$Solution
According to the question, two charges are separated by a distance 30cm and they repel each other by force 1N. Hence we can conclude that there is Coulomb’s force and by using Coulomb’s law we can find the value of the charges. The sum of the two charges is also given by which we can find the exact values.
Formula used:
F=4πε01r2q1q2
Complete answer:
According to Coulomb’s law, if two point charges q1 and q2 are separated by a distance r then the F will be given as
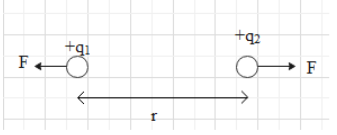
F=4πε01r2q1q2
Here ε0is the permittivity in free space and its value is 8.85×10−12Fm−1.
If both point charges have the same charge (i.e. negative or positive) they will repel and in case opposite charges are placed then they will attract.
According to the question, two point charges whose sum is 7μC are placed at distance 30cm and they have a repulsive force of 1N in between them. Let us suppose the point charges are q1 and q2and from the given dataF=1N,r=30cm=0.3m and ε0=8.85×10−12Fm−1. Then from the Coulomb’s law we can write,
