Question
Question: The sum of these three vectors is: 
Solution
Hint : As we can see in the given figure that, there are a total three vectors. So, first of all we will write each vector in their x-component and y-component and then we will add all the x-component and y-component to get the x, y component of the resultant vector of sum of these three vectors.
Complete step-by-step answer :
We have been asked to find the sum of three vectors as shown below,
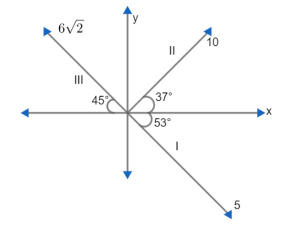
Let, the vectors name as I, II and III as shown in the figure.
Now, we will write each vector in their x-component and y-component as below,
For vector I, we have
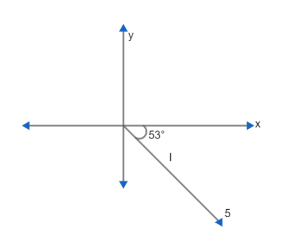
x-component ⇒5cos53∘
Since, we know that cos53∘=53
⇒x-component=5×53=3
y-component ⇒−5sin53∘
Using the value of sin53∘=54
⇒y-component=-5×54=−4
For vector II, we have
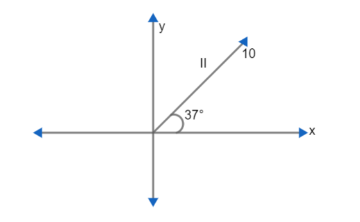
x-component ⇒10cos37∘
Using the value of cos37∘=54
⇒x-component=10×54=8
y-component ⇒10sin37∘
Using the value of sin37∘=53
⇒y-component=10×53=6
For vector III, we have
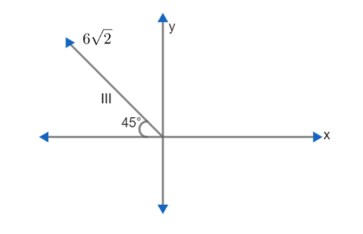
x-component ⇒−62cos45∘
Using the value of cos45∘=21
⇒x-component=-62×21=−6
y-component ⇒62sin45∘
Using the value of sin45∘=21
⇒y-component=62×21=6
Now, the x-component of the sum of all the three vectors is equal to the sum of the x-component of each vector.
x-component of resultant vector ⇒3+8−6=5
Similarly, y-component of resultant vector ⇒−4+6+6=8
Hence, the resultant vector will be 5i+8j
So, the correct answer is “Option D”.
Note : Be careful while finding the x and y components of the vector, as there is a chance that you might make a sign mistake. So, take care of the quadrant in which the vector lies. Also, you can use another method in which you add the two vectors first and the resultant will be added with the third resultant.
