Question

The sum of the series $\frac{1}{x+1}+\frac{2}{x^2+1}+\frac{2^2}{x^4+1}+....+\frac{2^{100}}{x^{2^{100}}+1}$ when x = 2 is:

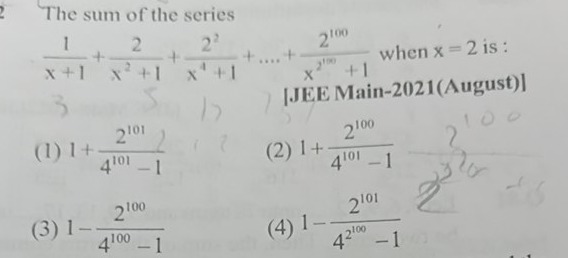
• A. 1+\frac{2^{101}}{4^{101}-1}
• B. 1+\frac{2^{100}}{4^{101}-1}
• C. 1-\frac{2^{100}}{4^{100}-1}
• D. 1-\frac{2^{101}}{4^{2^{100}}-1}

Answer 1

Answer: (D)

1-\frac{2^{101}}{4^{2^{100}}-1}

Answer 2

The given series is $S = \frac{1}{x+1}+\frac{2}{x^2+1}+\frac{2^2}{x^4+1}+....+\frac{2^{100}}{x^{2^{100}}+1}$. This can be written as $S = \sum_{n=0}^{100} \frac{2^n}{x^{2^n}+1}$.

We use the identity: $\frac{2^n}{y+1} = \frac{2^n}{y-1} - \frac{2^{n+1}}{y^2-1}$ Let $y = x^{2^n}$. Then $y^2 = (x^{2^n})^2 = x^{2 \cdot 2^n} = x^{2^{n+1}}$. Substituting this into the identity, we get: $\frac{2^n}{x^{2^n}+1} = \frac{2^n}{x^{2^n}-1} - \frac{2^{n+1}}{x^{2^{n+1}}-1}$ Let $a_n = \frac{2^n}{x^{2^n}-1}$. Then the general term of the series can be written as $T_n = a_n - a_{n+1}$.

The sum of the series is a telescoping sum: $S = \sum_{n=0}^{100} T_n = \sum_{n=0}^{100} (a_n - a_{n+1})$ $S = (a_0 - a_1) + (a_1 - a_2) + (a_2 - a_3) + \dots + (a_{100} - a_{101})$ $S = a_0 - a_{101}$ Now, we find $a_0$ and $a_{101}$: $a_0 = \frac{2^0}{x^{2^0}-1} = \frac{1}{x^1-1} = \frac{1}{x-1}$ $a_{101} = \frac{2^{101}}{x^{2^{101}}-1}$

So, the sum is: $S = \frac{1}{x-1} - \frac{2^{101}}{x^{2^{101}}-1}$ We are given $x=2$. Substituting $x=2$: $S = \frac{1}{2-1} - \frac{2^{101}}{2^{2^{101}}-1}$ $S = 1 - \frac{2^{101}}{2^{2^{101}}-1}$ To match the options, we rewrite the term $2^{2^{101}}$: $2^{2^{101}} = 2^{(2 \cdot 2^{100})} = (2^2)^{2^{100}} = 4^{2^{100}}$. Therefore, the sum is: $S = 1 - \frac{2^{101}}{4^{2^{100}}-1}$