Question
Question: The sum of the series $\frac{1}{x+1}+\frac{2}{x^2+1}+\frac{2^2}{x^4+1}+....+\frac{2^{100}}{x^{2^{100...
The sum of the series x+11+x2+12+x4+122+....+x2100+12100 when x = 2 is: [JEE Main-2021(August)]
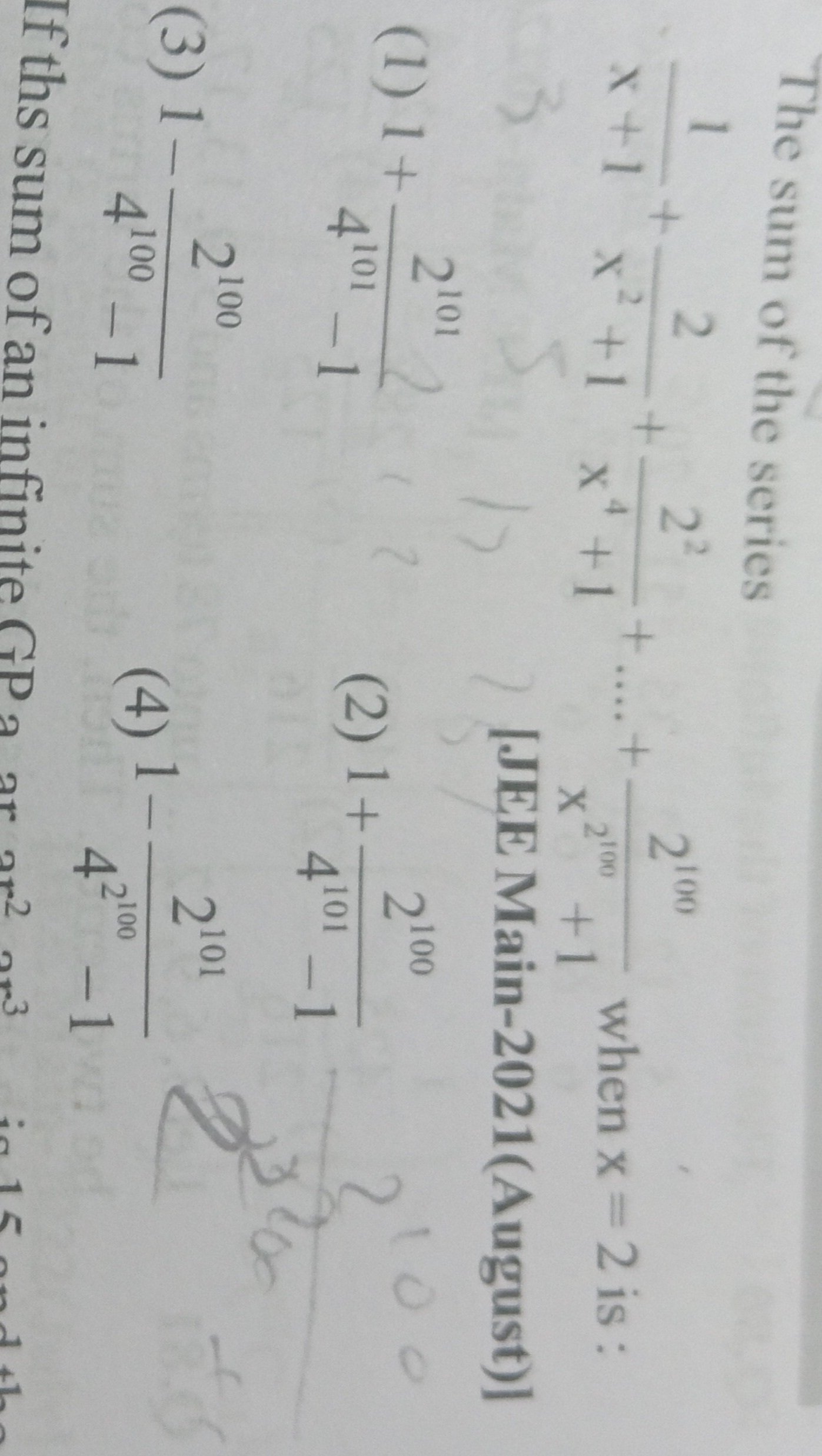
1+4101−12101
1+4101−12100
1-4100−12100
1-42100−12101
1-42100−12101
Solution
The given series is S=x+11+x2+12+x4+122+....+x2100+12100. This can be written in summation notation as S=∑k=0100x2k+12k.
We use the algebraic identity: y−11−y+11=(y−1)(y+1)(y+1)−(y−1)=y2−12. Rearranging this identity to isolate the term with (y+1) in the denominator, we get: y+11=y−11−y2−12.
Let y=x2k. Then y2=(x2k)2=x2⋅2k=x2k+1. Substituting y=x2k into the rearranged identity: x2k+11=x2k−11−x2k+1−12.
Now, multiply both sides by 2k to match the numerator of the terms in our series: x2k+12k=x2k−12k−x2k+1−12k⋅2=x2k−12k−x2k+1−12k+1.
Now, we can write the sum S using this expression: S=∑k=0100(x2k−12k−x2k+1−12k+1).
This is a telescoping sum. Let Ak=x2k−12k. The sum becomes ∑k=0100(Ak−Ak+1). The sum of such a series is A0−A101.
A0=x20−120=x1−11=x−11. A101=x2101−12101.
So, the sum of the series is: S=x−11−x2101−12101.
We are asked to find the sum when x=2. Substitute x=2 into the formula: S=2−11−22101−12101 S=1−22101−12101.
Let's simplify the denominator of option (4): 42100−1=(22)2100−1=22⋅2100−1=22101−1. So, option (4) is 1−22101−12101.
This matches our derived sum.
