Question
Question: The sum of the series $2 \times 1 \times {}^{20}C_4 - 3 \times 2 \times {}^{20}C_5 + 4 \times 3 \tim...
The sum of the series 2×1×20C4−3×2×20C5+4×3×20C6−5×4×20C7+...+18×17×20C20, is equal to
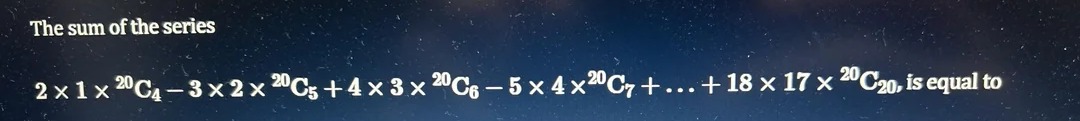
34
Solution
Let S=2×1×20C4−3×2×20C5+4×3×20C6−5×4×20C7+⋯+18×17×20C20.
We can write the general term of the series as Tn=(−1)n−4(n−2)(n−3)20Cn, where n ranges from 4 to 20. So, S=∑n=420(−1)n−4(n−2)(n−3)20Cn.
Consider the expansion of (1−x)20: (1−x)20=∑k=020(−1)k20Ckxk.
Differentiate twice with respect to x: First derivative: dxd(1−x)20=−20(1−x)19=∑k=120(−1)kk20Ckxk−1.
Second derivative: dx2d2(1−x)20=−20(−19)(1−x)18=20×19(1−x)18. On the right side: ∑k=220(−1)kk(k−1)20Ckxk−2.
So, 20×19(1−x)18=∑k=220(−1)kk(k−1)20Ckxk−2.
Let j=k−2. Then k=j+2. When k=2, j=0. When k=20, j=18. 20×19(1−x)18=∑j=018(−1)j+2(j+2)(j+1)20Cj+2xj. Since (−1)j+2=(−1)j, we have: 20×19(1−x)18=∑j=018(−1)j(j+2)(j+1)20Cj+2xj.
Let's use the identity k(k−1)NCk=N(N−1)N−2Ck−2. Consider the sum S=∑n=420(−1)n−4(n−2)(n−3)20Cn. Let j=n−4. Then n=j+4. S=∑j=016(−1)j(j+2)(j+1)20Cj+4.
Let's use the general form: ∑k=rn(−1)k−rf(k)NCk. Consider the identity ∑k=rN(−1)kNCkP(k)=0 if P(k) is a polynomial of degree less than N−r. This is not directly applicable.
Let's recall the identity: ∑k=0n(−1)knCk=0 for n≥1. ∑k=0n(−1)kknCk=0 for n≥2. ∑k=0n(−1)kk(k−1)nCk=0 for n≥3. In general, ∑k=0n(−1)kk(k−1)…(k−m+1)nCk=0 for n≥m+1.
Let's consider the sum S=∑n=420(−1)n−4(n−2)(n−3)20Cn. Let k=n−4. Then the sum becomes S=∑k=016(−1)k(k+2)(k+1)20Ck+4.
Let's use the property: k(k−1)…(k−m+1)NCk=N(N−1)…(N−m+1)N−mCk−m. We have (n−2)(n−3)20Cn.
Now, let's consider the sum Sfull=∑n=020(−1)n(n−2)(n−3)20Cn. Sfull=∑n=020(−1)n[n(n−1)−4n+6]20Cn. Sfull=∑n=020(−1)nn(n−1)20Cn−4∑n=020(−1)nn20Cn+6∑n=020(−1)n20Cn.
For N=20:
- ∑n=020(−1)n20Cn=0 (since 20≥1).
- ∑n=020(−1)nn20Cn=0 (since 20≥2).
- ∑n=020(−1)nn(n−1)20Cn=0 (since 20≥3).
Therefore, Sfull=0−4(0)+6(0)=0.
Now, let's relate Sfull to the given series S. The given series is S=∑n=420(−1)n−4(n−2)(n−3)20Cn.
For n=0,1,2,3, the terms in Sfull are: For n=0: (−1)0(0−2)(0−3)20C0=1×6×1=6. For n=1: (−1)1(1−2)(1−3)20C1=−1×(−1)×(−2)×20=−40. For n=2: (−1)2(2−2)(2−3)20C2=1×0×(−1)×20C2=0. For n=3: (−1)3(3−2)(3−3)20C3=−1×1×0×20C3=0.
So, Sfull=6−40+0+0+∑n=420(−1)n(n−2)(n−3)20Cn=0. −34+∑n=420(−1)n(n−2)(n−3)20Cn=0. So, ∑n=420(−1)n(n−2)(n−3)20Cn=34.
Our given series is S=∑n=420(−1)n−4(n−2)(n−3)20Cn. The signs in S are (−1)n−4. The signs in the sum we just calculated are (−1)n. Since (−1)n−4=(−1)n(−1)−4=(−1)n×1=(−1)n. So, the signs are the same for n≥4.
Therefore, S=∑n=420(−1)n(n−2)(n−3)20Cn=34.
