Question

The sum of the magnitudes of two vectors is 18. The magnitude of their resultant is 12. If the resultant is perpendicular to one of the vectors, find the magnitudes of the two vectors.

Answer 1

The resultant vector results from the combination of two or more vectors. Magnitude of a vector is the value assigned to it, irrespective of its direction.
$\Rightarrow {A^2} + {B^2} = {C^2}$ is the equation for the Pythagoras theorem. Here, A and B are the two sides of a right triangle and C is the hypotenuse.

Complete step by step answer:
In this question, we are provided with the resultant magnitude of two vectors. We also know the sum of the magnitudes of the two vectors. We are asked to find the magnitudes of the two vectors independently. Let us assume the magnitudes of the two vectors are denoted by A and B, and their resultant is denoted by R. The data about these given to us is:
$\Rightarrow A + B = 18$
Writing one of the vectors in the terms of another gives us:
$\Rightarrow B = 18 - A$
The resultant vector magnitude is 12, and its alignment is 90 degrees to one of the vectors. This follows the formation of a right angled triangle.
We know that the Pythagoras theorem can be used to find the values of the sides of a right triangle as:
$\Rightarrow {A^2} + {B^2} = {C^2}$

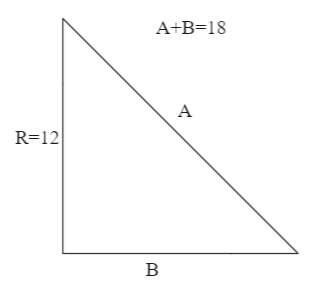
From the figure, we can see that the hypotenuse is $A$, base is $18 - A$and the perpendicular is $R$. Putting these values in the equation gives us:
$\Rightarrow {A^2} = {(18 - A)^2} + {R^2}$
$\Rightarrow {A^2} = {(18 - A)^2} + {12^2}$
Expanding the brackets and solving for A gives us:
$\Rightarrow {A^2} = 324 - 36A + {A^2} + 144$
$\Rightarrow 36A = 468$
This provides with the magnitude of $A = 13$
To find the magnitude of the other vector, we know that:
$\Rightarrow B = 18 - A = 18 - 13 = 5$
Hence, the magnitudes of the two vectors are 13 and 5.

Note:
The Pythagoras theorem is very handy because of its easy formulation. It adds another property to the existing triangle, hence it should be looked out for. If anything forms a right angled triangle, it should immediately be noted whether or not Pythagoras theorem can help.