Solveeit Logo
Login

Question

Question: The sum of real roots of the equation \({{x}^{2}}+5\left| x \right|+6=0\) is A. 5 B. 10 C. -5 ...

The sum of real roots of the equation x2+5∣x∣+6=0{{x}^{2}}+5\left| x \right|+6=0 is
A. 5
B. 10
C. -5
D. None of these.

Explanation

Solution

Hint: Solve for cases when x>0 and x≤0x\le 0 individually and remove extraneous roots(means which does not satisfy two cases). Use property that |x| = x when x>0 and |x| = -x when x≤0x\le 0. Find the sum of all the real roots found. Alternatively, you can plot the given function and find the points at which the graph of the given function intersects the x-axis.

“Complete step-by-step answer:”
We will solve the above question for two cases.
Case I: x>0
We have |x| = x
⇒x2+5x+6=0\Rightarrow {{x}^{2}}+5x+6=0
Using the quadratic formula which states that for quadratic equation ax2+bx+c=0a{{x}^{2}}+bx+c=0 the roots are x=−b±b2−4ac2ax=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}
Here a = 1, b = 5 and c = 6
Using the quadratic formula, we get
x=−5±52−4(1)(6)2(1) ⇒x=−5±25−242 ⇒x=−5±12=−5±12 ⇒x=−5+12 or x=−5−12 ⇒x=−2 or x=−3 \begin{aligned} & x=\dfrac{-5\pm \sqrt{{{5}^{2}}-4\left( 1 \right)\left( 6 \right)}}{2\left( 1 \right)} \\\ & \Rightarrow x=\dfrac{-5\pm \sqrt{25-24}}{2} \\\ & \Rightarrow x=\dfrac{-5\pm \sqrt{1}}{2}=\dfrac{-5\pm 1}{2} \\\ & \Rightarrow x=\dfrac{-5+1}{2}\text{ or }x=\dfrac{-5-1}{2} \\\ & \Rightarrow x=-2\text{ or }x=-3 \\\ \end{aligned}
Since x>0 both x = -2 and x = -3 are extraneous roots.
Case II: x≤0x\le 0
We have |x| = -x
⇒x2−5x+6=0\Rightarrow {{x}^{2}}-5x+6=0
Here a = 1, b = -5 and c = 6
Using the quadratic formula, we get
x=−(−5)±(−5)2−4(1)(6)2(1) ⇒x=5±25−242 ⇒x=5±12=5±12 ⇒x=5+12 or x=5−12 ⇒x=3 or x=2 \begin{aligned} & x=\dfrac{-\left( -5 \right)\pm \sqrt{{{\left( -5 \right)}^{2}}-4\left( 1 \right)\left( 6 \right)}}{2\left( 1 \right)} \\\ & \Rightarrow x=\dfrac{5\pm \sqrt{25-24}}{2} \\\ & \Rightarrow x=\dfrac{5\pm \sqrt{1}}{2}=\dfrac{5\pm 1}{2} \\\ & \Rightarrow x=\dfrac{5+1}{2}\text{ or }x=\dfrac{5-1}{2} \\\ & \Rightarrow x=3\text{ or }x=2 \\\ \end{aligned}
Since x≤0x\le 0, both x = 3 and x =2 are extraneous roots.
Hence the given equation has no real roots
Hence option D is correct.

Note: Alternative solution:
If we know the graph of f(x) then the graph of f(|x|) is the same as the graph f(x) for x>0 and for x≤0x\le 0 the graph is the mirror image taken in the y-axis.
Let f(x)=x2+5x+6f(x)={{x}^{2}}+5x+6
Then f(∣x∣)=x2+5∣x∣+6f\left( \left| x \right| \right)={{x}^{2}}+5\left| x \right|+6
First, we draw the graph of f(x)

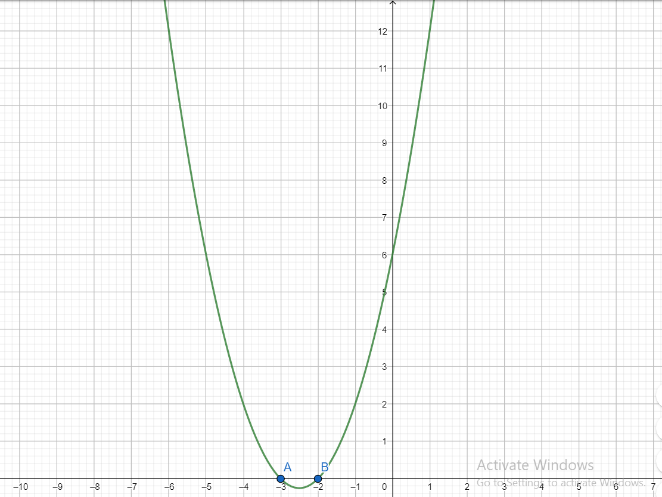
Then using the above-mentioned fact, we draw the graph of f(|x|)

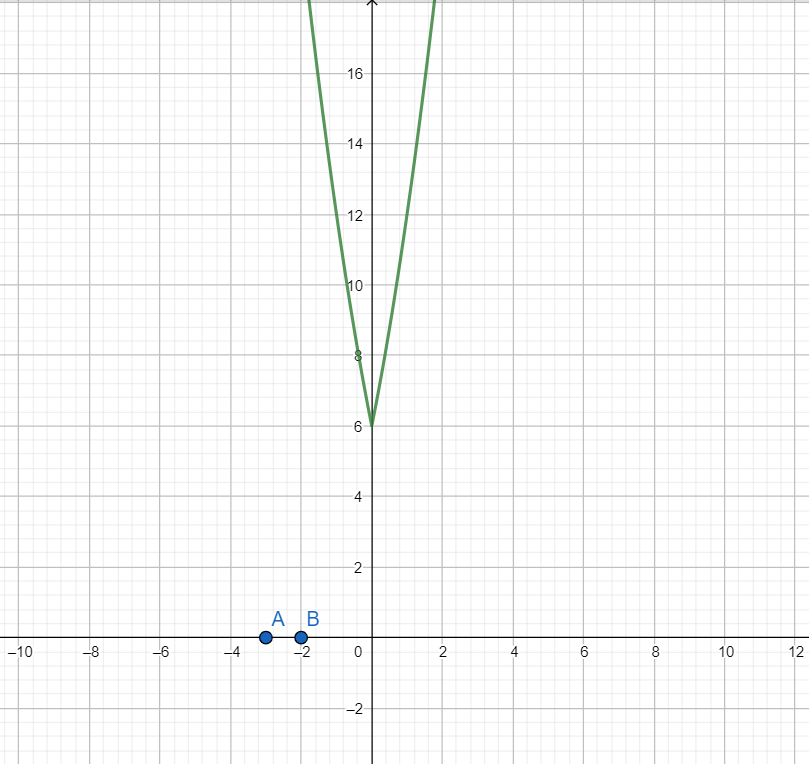
As is evident from the graph, the function f(|x|) does not have any root because it does not intersect the x-axis.
Hence the given equation x2+5∣x∣+6=0{{x}^{2}}+5\left| x \right|+6=0 has no real roots.