Question

The sum of magnitude of two forces acting at a point is $16N$. If the resultant force is $8N$ and its direction is perpendicular to smaller force, then the forces are:
$\left( A \right)6N\,\,and\,\,10N$
$\left( B \right)8N\,\,and\,\,8N$
$\left( C \right)4N\,\,and\,\,12N$
$\left( D \right)2N\,\,and\,\,14N$

Answer 1

First of all we have to draw a rough diagram representing all the required vectors and angles between them. Now using trigonometric formulas for the angle that is perpendicular to the smaller force and from that we can find the angle between the two forces. Finally using the resultant formula and putting the value of sum of magnitude and the angle between them then we can find the two forces.

Complete step by step answer:
As per the problem we know the sum of magnitude of two forces acting at a point is $16N$. If the resultant force is $8N$ and its direction is perpendicular to the smaller force.
Now we need to find the two forces.
Let us assume that the two forces are A and B where A is the smaller force and the resultant vector is perpendicular to it.
And from the problem,
Sum of the magnitude of two forces is equal to $16N$.
Mathematically,
$\overrightarrow A + \overrightarrow B = 16N \ldots \ldots \left( 1 \right)$
And we know,
$\overrightarrow R = 8N \ldots \ldots \left( 2 \right)$

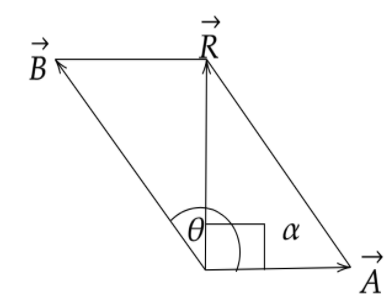
Now from the figure we can say that,
$\alpha = 90^\circ$
$\theta$ is the angle between the two forces.
Now from figure using trigonometric formula we can write,
$\tan \alpha = \dfrac{{B\sin \theta }}{{A + B\cos \theta }}$
Where, $\tan \alpha = \dfrac{{Perpendicular}}{{Base}}$
On putting $\alpha = 90^\circ$ we will get,
$\infty = \dfrac{{B\sin \theta }}{{A + B\cos \theta }}$
We can write infinity as $\dfrac{1}{0}$.
Hence we will get,
$A + B\cos \theta = 0$
Now after rearranging we will get,
$\cos \theta = - \dfrac{A}{B} \ldots \ldots \left( 3 \right)$
Now using resultant formula we will get,
$R = \sqrt {{A^2} + {B^2} + 2AB\cos \theta }$
Now putting equation $\left( 2 \right)\,{\text{and}}\,\left( 3 \right)$ in the above formula we will get,
$8 = \sqrt {{A^2} + {B^2} + 2AB\left( { - \dfrac{A}{B}} \right)}$
Cancelling the common terms we will get,
$8 = \sqrt {{A^2} + {B^2} - 2{A^2}}$
$64 = {B^2} - {A^2}$
We know, ${a^2} - {b^2} = \left( {a + b} \right)\left( {a - b} \right)$
Now putting the above formula and using equation $\left( 1 \right)$ we will get,
$B - A = 4N \ldots \ldots \left( 4 \right)$
Now adding and subtracting equation $\left( 1 \right)\,{\text{and}}\,\left( 4 \right)$ we will get,
$\overrightarrow A = 6N$
And $\overrightarrow B = 10N$.
Therefore the correct option is (A).

Note: Remember that the resultant is the vector sum of two or more vectors and it is the result of adding two or more vectors at a time that are connected to each other at some angle. Note that if two or more velocity vectors are added then the resultant is also a velocity vector. It means addition of the same kind of vectors is possible and the resultant vector is also the same as that or the added vectors.