Question

The sum of infinite series

$\frac{1}{15} + \frac{1}{30} + \frac{1}{50} + \frac{1}{75} + ......\infty$ is $\frac{k}{20}$, then the value of k is

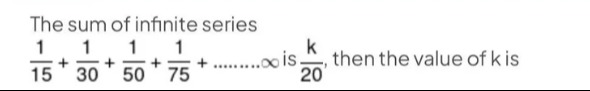
Answer 1

k = 4

Answer 2

Given the series

$\frac{1}{15}+\frac{1}{30}+\frac{1}{50}+\frac{1}{75}+\cdots,$

we first express the general term. Notice the denominators follow a quadratic pattern. Writing the $n$th term as

$a_n = \frac{1}{d_n},\quad d_n = \frac{5n^2+15n+10}{2},$

we have

$a_n = \frac{2}{5n^2+15n+10} = \frac{2}{5(n+1)(n+2)}.$

Thus,

$a_n = \frac{2}{5}\cdot\frac{1}{(n+1)(n+2)}.$

Step 1: Partial Fraction Decomposition

Decompose:

$\frac{1}{(n+1)(n+2)} = \frac{1}{n+1} - \frac{1}{n+2},$

so that

$a_n = \frac{2}{5}\left(\frac{1}{n+1} - \frac{1}{n+2}\right).$

Step 2: Telescoping Series Sum

The sum of the series becomes:

$S = \frac{2}{5} \sum_{n=1}^\infty \left(\frac{1}{n+1} - \frac{1}{n+2}\right).$

Writing the partial sum $S_N$:

$S_N = \frac{2}{5} \left[\left(\frac{1}{2} - \frac{1}{3}\right) + \left(\frac{1}{3} - \frac{1}{4}\right) + \cdots + \left(\frac{1}{N+1} - \frac{1}{N+2}\right)\right].$

This telescopes to:

$S_N = \frac{2}{5} \left(\frac{1}{2} - \frac{1}{N+2}\right).$

Taking $N \to \infty$,

$S = \frac{2}{5}\cdot\frac{1}{2} = \frac{1}{5}.$

Given that the sum is also expressed as $\frac{k}{20}$, equate:

$\frac{1}{5} = \frac{k}{20} \quad\Longrightarrow\quad k = 4.$