Question

The sufficient conditions for the function $f:R \to R$ is to be maximum at $x = a$ will be
$\left( 1 \right)f'\left( a \right) = 0{\text{ and }}f''\left( a \right) > 0$
$\left( 2 \right)f'\left( a \right) = 0{\text{ and }}f''\left( a \right) = 0$
$\left( 3 \right)f'\left( a \right) = 0{\text{ and }}f''\left( a \right) < 0$
$\left( 4 \right)f'\left( a \right) > 0{\text{ and }}f''\left( a \right) < 0$

Answer 1

This question deals with the concepts of maximum and minimum values for a function in a given domain. In addition to this, we must be familiar with the necessary and sufficient conditions for a function to be maximum or minimum. The maxima or minima are also called as extreme values for a function. Let $y = f\left( x \right)$ is a function in a single variable $x$ defined in the domain of $x$ . During the interval of $x$ on which the function attains the extreme value , the extreme values can be termed as local or global.

Complete step-by-step solution:
The figure shown below represents the various types of extreme values for a function. Let us understand the basic terminology first ;

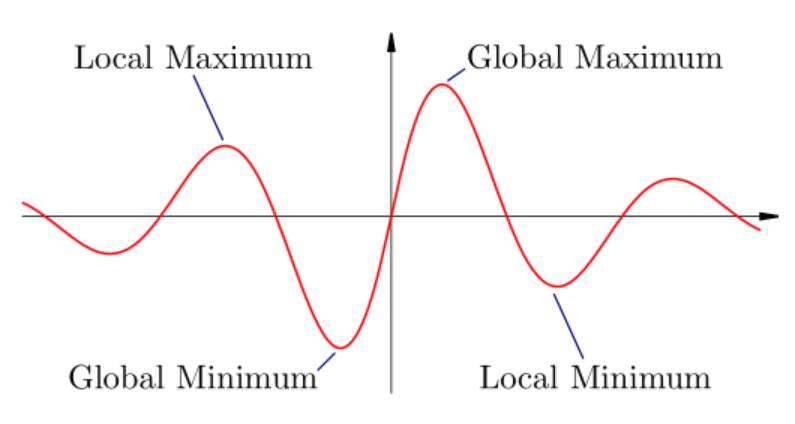
Figure $\left( 1 \right)$ : Types of extreme values for a function
$\left( 1 \right)$ Local Maxima: A point in the domain of $x$ is called a local maximum when there can be some other point for which the value of function may be more than the value of local maxima.
$\left( 2 \right)$ Global Maxima: The highest peak value in the domain of $x$ is called global maxima , the function at any point in the domain can not exceed this value.
$\left( 3 \right)$ Local Minima: : A point in the domain of $x$ is called local minima when there can be some other point for which the value of function may be even less than the value of local minima.
$\left( 4 \right)$ Global Minima: The lowest peak value in the domain of $x$ is called global minima , the value of the function at any point in the domain can not be lower than this value.
$\left( 5 \right)$ Critical point or stationary point: A point on the curve where the derivative is zero i.e. ${\left. {\dfrac{d}{{dx}}f\left( x \right)} \right|_{x = c}} = 0$ , where c is the critical point. There are three types of critical or stationary points: Local maxima , Local minima and inflection point.
$\left( 6 \right)$ Inflection point: A point on the curve is called point of inflection when we can not conclude whether it is a point of relative maxima or relative minima even if $f'\left( c \right) = 0$ . For example : $f\left( x \right) = {x^3}$ , $\dfrac{d}{{dx}}{x^3} = 3{x^2}$ means $f'\left( x \right) = 3{x^2}$ . At $x = 0$ , the function is neither maximum nor minimum as shown in the figure below:

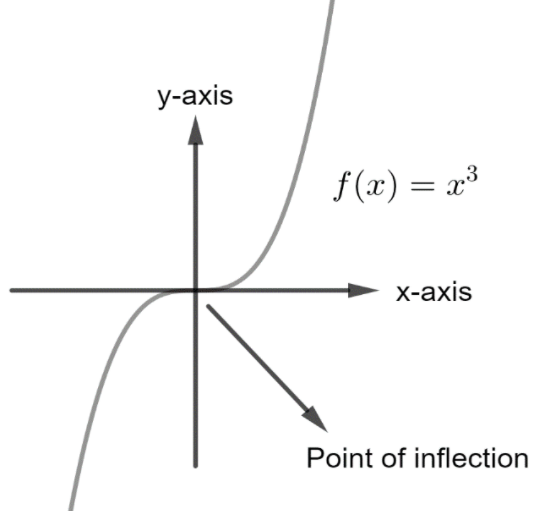
Figure $\left( 2 \right)$ : Point of Inflection
The sufficient conditions for a function to be maximum or minimum at any critical point c are given by the second derivative test as ;
If $f'{\left( x \right)_{x = c}} = f''{\left( x \right)_{x = c}} = ......{f^{n - 1}}{\left( x \right)_{x = c}} = 0$ and ${f^n}\left( {{x^n}} \right) \ne 0$ , then $x = c$ is said to be :
$\left( 1 \right)$ Relative minimum if ${f^n}{\left( x \right)_{x = c}} > 0$ and n is even .
$\left( 2 \right)$ Relative maximum if ${f^n}{\left( x \right)_{x = c}} < 0$ and n is even .
$\left( 3 \right)$ Point of inflection if n is odd.
According to the question; $x = a$ is the critical point and we are asked about the sufficient conditions for the function to be maximum. By using the above statements for sufficient conditions we can say that the $f'\left( a \right) = 0{\text{ and }}f''\left( a \right) < 0$ is the correct statement.
Therefore, the correct answer for this question is option $\left( 3 \right)$ .

Note: The necessary conditions for a function $y = f\left( x \right)$ is, if point of maxima or point of minima exists then $f'{\left( x \right)_{x = c}} = 0$ where c is the critical point meaning that the given function must be differentiable with respect to the independent variable and then by equating the first derivative of the function with zero , we will get the possible values of the roots. The next step is to follow the second derivative test and use that to find the maxima and minima for the given function.