Question

The stress versus strain graphs for wires of two materials A and B are as shown in the figure.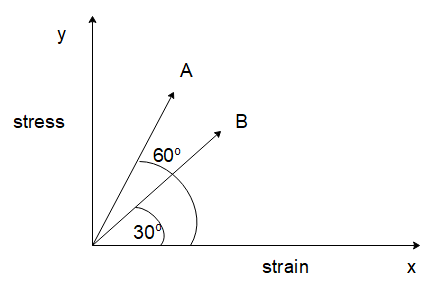

If ${Y_A}$ ​ and ${Y_B}$ ​ are the Young’s moduli of the materials, then ​
A) ${Y_B} = 2{Y_A}$
B) ${Y_A} = {Y_B}$
C) ${Y_B} = 3{Y_A}$
D) ${Y_A} = 3{Y_B}$

Answer 1

Hint : The young’s modulus of wire is the slope of the line of the wire in the graph of stress versus strain. The slope of a line can be determined using the angle the line makes with the $x$ -axis.

Complete step by step answer
We know that the slope of the line in a stress-strain curve represents the young’s modulus for a wire. We also know that the slope of a line can be calculated as the tangent of the angle the line makes with the positive x-axis of the graph.
So, for wire A, the stress-strain line of the material is at an angle of $60^\circ$ from the positive $x$ -axis. So the slope of the line $({m_A})$ will be
${m_A} = \tan 60^\circ$
$\Rightarrow {m_A} = \sqrt 3$
Hence the young’s modulus of wire A will also be $\sqrt 3$ .
Similarly, for wire B, the stress-strain line of the material is at an angle of $30^\circ$ from the positive $x$ -axis. So, the slope of the line $({m_B})$ will be
${m_B} = \tan 30^\circ$
$\Rightarrow {m_B} = \dfrac{1}{{\sqrt 3 }}$
Hence the young’s modulus of wire B will also be $1/\sqrt 3$ .
Then taking the ratio of the young’s modulus for wire A and B, we get
$\dfrac{{{Y_A}}}{{{Y_B}}} = \dfrac{{\sqrt 3 }}{{1/\sqrt 3 }}$
$\therefore \dfrac{{{Y_A}}}{{{Y_B}}} = 3$
Hence, we can write
${Y_A} = 3{Y_B}$ which corresponds to option (D) which is the correct choice.

Note
We can only calculate the slope of the line in such a way if the stress-strain curve for a wire is a straight line. For practical wires, the stress-strain curve is linear only for a range of values of stress applied on the wire. While calculating the slope of the wire, we must calculate the tangent of the line made with the $x$ -axis and not the $y$ -axis if the strain is represented on the $x$ -axis of the graph.