Solveeit Logo
Login

Question

Question: The straight lines represented by \[{\left( {y - mx} \right)^2} = {a^2}\left( {1 + {m^2}} \right)\] ...

The straight lines represented by (y−mx)2=a2(1+m2){\left( {y - mx} \right)^2} = {a^2}\left( {1 + {m^2}} \right) and (y−nx)2=a2(1+n2){\left( {y - nx} \right)^2} = {a^2}\left( {1 + {n^2}} \right) form a
(a) rectangle
(b) rhombus
(c) trapezium
(d) None of these

Explanation

Solution

Here, we need to find the shape formed by the given straight lines equation. First, we will take the square root of the two equations and simplify it to find the equations of the four lines required to form a shape. These lines are linear equations in two variables. We will compare the ratios of the coefficients of two lines to get the pair of parallel lines. Then, we will use the distance formula between two parallel lines to find the two altitudes of the quadrilateral. Finally, we will use the formula for the area of a parallelogram to find the shape of the quadrilateral formed.

Formula Used:
We will use the following formulas:
1. The linear equations in two variables a1x+b1y+c1=0{a_1}x + {b_1}y + {c_1} = 0 and a2x+b2y+c2=0{a_2}x + {b_2}y + {c_2} = 0 have no solution if a1a2=b1b2≠c1c2\dfrac{{{a_1}}}{{{a_2}}} = \dfrac{{{b_1}}}{{{b_2}}} \ne \dfrac{{{c_1}}}{{{c_2}}}.
2. The distance between two parallel lines ax+by+c1=0ax + by + {c_1} = 0 and ax+by+c2=0ax + by + {c_2} = 0 is given by the formula d=∣c2−c1∣a2+b2d = \dfrac{{\left| {{c_2} - {c_1}} \right|}}{{\sqrt {{a^2} + {b^2}} }}.

Complete step-by-step answer:
First, we will find the straight lines by simplifying the given equations.
Taking the square root of both sides of the equation (y−mx)2=a2(1+m2){\left( {y - mx} \right)^2} = {a^2}\left( {1 + {m^2}} \right), we get
⇒(y−mx)2=a2(1+m2) ⇒y−mx=±a1+m2\begin{array}{l} \Rightarrow \sqrt {{{\left( {y - mx} \right)}^2}} = \sqrt {{a^2}\left( {1 + {m^2}} \right)} \\\ \Rightarrow y - mx = \pm a\sqrt {1 + {m^2}} \end{array}
Thus, we get the equations
⇒y−mx=a1+m2\Rightarrow y - mx = a\sqrt {1 + {m^2}} and y−mx=−a1+m2y - mx = - a\sqrt {1 + {m^2}}
Let the straight lines represented by the equations y−mx=a1+m2y - mx = a\sqrt {1 + {m^2}} and y−mx=−a1+m2y - mx = - a\sqrt {1 + {m^2}} be pp and qq respectively.
Now, we will check the number of solutions of the lines pp and qq.
We can observe that the lines y−mx=a1+m2y - mx = a\sqrt {1 + {m^2}} and y−mx=−a1+m2y - mx = - a\sqrt {1 + {m^2}} are linear equations in two variables.
The linear equations in two variables a1x+b1y+c1=0{a_1}x + {b_1}y + {c_1} = 0 and a2x+b2y+c2=0{a_2}x + {b_2}y + {c_2} = 0 have unique solution if a1a2≠b1b2\dfrac{{{a_1}}}{{{a_2}}} \ne \dfrac{{{b_1}}}{{{b_2}}}.
The linear equations in two variables a1x+b1y+c1=0{a_1}x + {b_1}y + {c_1} = 0 and a2x+b2y+c2=0{a_2}x + {b_2}y + {c_2} = 0 have infinitely many solutions if a1a2=b1b2=c1c2\dfrac{{{a_1}}}{{{a_2}}} = \dfrac{{{b_1}}}{{{b_2}}} = \dfrac{{{c_1}}}{{{c_2}}}.
The linear equations in two variables a1x+b1y+c1=0{a_1}x + {b_1}y + {c_1} = 0 and a2x+b2y+c2=0{a_2}x + {b_2}y + {c_2} = 0 have no solution if a1a2=b1b2≠c1c2\dfrac{{{a_1}}}{{{a_2}}} = \dfrac{{{b_1}}}{{{b_2}}} \ne \dfrac{{{c_1}}}{{{c_2}}}.
Rewriting the equations of the lines, we get
−mx+y−a1+m2=0- mx + y - a\sqrt {1 + {m^2}} = 0 and −mx+y+a1+m2=0 - mx + y + a\sqrt {1 + {m^2}} = 0
Comparing −mx+y−a1+m2=0 - mx + y - a\sqrt {1 + {m^2}} = 0 to the standard form a1x+b1y+c1=0{a_1}x + {b_1}y + {c_1} = 0, we get
a1=−m{a_1} = - m, b1=1{b_1} = 1, and c1=−a1+m2{c_1} = - a\sqrt {1 + {m^2}}
Comparing −mx+y+a1+m2=0 - mx + y + a\sqrt {1 + {m^2}} = 0 to the standard form a2x+b2y+c2=0{a_2}x + {b_2}y + {c_2} = 0, we get
a2=−m{a_2} = - m, b2=1{b_2} = 1, and c2=a1+m2{c_2} = a\sqrt {1 + {m^2}}
Now, we will find the ratios of the coefficients of xx, yy, and the constant.
Dividing a1=−m{a_1} = - m by a2=−m{a_2} = - m, we get
a1a2=−m−m=1\dfrac{{{a_1}}}{{{a_2}}} = \dfrac{{ - m}}{{ - m}} = 1
Dividing b1=1{b_1} = 1 by b2=1{b_2} = 1, we get
b1b2=11=1\dfrac{{{b_1}}}{{{b_2}}} = \dfrac{1}{1} = 1
Dividing c1=−a1+m2{c_1} = - a\sqrt {1 + {m^2}} by c2=a1+m2{c_2} = a\sqrt {1 + {m^2}} , we get
c1c2=−a1+m2a1+m2=−1\dfrac{{{c_1}}}{{{c_2}}} = \dfrac{{ - a\sqrt {1 + {m^2}} }}{{a\sqrt {1 + {m^2}} }} = - 1
We can observe that a1a2=b1b2≠c1c2\dfrac{{{a_1}}}{{{a_2}}} = \dfrac{{{b_1}}}{{{b_2}}} \ne \dfrac{{{c_1}}}{{{c_2}}}.
Therefore, the lines −mx+y−a1+m2=0 - mx + y - a\sqrt {1 + {m^2}} = 0 and −mx+y+a1+m2=0 - mx + y + a\sqrt {1 + {m^2}} = 0 have no solution.
This means that the lines pp and qq are parallel lines.
Taking the square root on both sides (y−nx)2=a2(1+n2){\left( {y - nx} \right)^2} = {a^2}\left( {1 + {n^2}} \right), we get
⇒(y−nx)2=a2(1+n2) ⇒y−nx=±a1+n2\begin{array}{l} \Rightarrow \sqrt {{{\left( {y - nx} \right)}^2}} = \sqrt {{a^2}\left( {1 + {n^2}} \right)} \\\ \Rightarrow y - nx = \pm a\sqrt {1 + {n^2}} \end{array}
Thus, we get the equations
⇒y−nx=a1+n2\Rightarrow y - nx = a\sqrt {1 + {n^2}} and y−nx=−a1+n2y - nx = - a\sqrt {1 + {n^2}}
Let the straight lines represented by the equations y−nx=a1+n2y - nx = a\sqrt {1 + {n^2}} and y−nx=−a1+n2y - nx = - a\sqrt {1 + {n^2}} be rr and ss respectively.
Now, we will check the number of solutions of the lines rr and ss.
We can observe that the lines y−nx=a1+n2y - nx = a\sqrt {1 + {n^2}} and y−nx=−a1+n2y - nx = - a\sqrt {1 + {n^2}} are linear equations in two variables.
Rewriting the equations of the lines, we get
−nx+y−a1+n2=0- nx + y - a\sqrt {1 + {n^2}} = 0 and −nx+y+a1+n2=0 - nx + y + a\sqrt {1 + {n^2}} = 0
Comparing −nx+y−a1+n2=0 - nx + y - a\sqrt {1 + {n^2}} = 0 to the standard form a1x+b1y+c1=0{a_1}x + {b_1}y + {c_1} = 0, we get
a1=−n{a_1} = - n, b1=1{b_1} = 1, and c1=−a1+n2{c_1} = - a\sqrt {1 + {n^2}}
Comparing −nx+y+a1+n2=0 - nx + y + a\sqrt {1 + {n^2}} = 0 to the standard form a2x+b2y+c2=0{a_2}x + {b_2}y + {c_2} = 0, we get
a2=−n{a_2} = - n, b2=1{b_2} = 1, and c2=a1+n2{c_2} = a\sqrt {1 + {n^2}}
Now, we will find the ratios of the coefficients of xx, yy, and the constant.
Dividing a1=−n{a_1} = - n by a2=−n{a_2} = - n, we get
a1a2=−n−n=1\dfrac{{{a_1}}}{{{a_2}}} = \dfrac{{ - n}}{{ - n}} = 1
Dividing b1=1{b_1} = 1 by b2=1{b_2} = 1, we get
b1b2=11=1\dfrac{{{b_1}}}{{{b_2}}} = \dfrac{1}{1} = 1
Dividing c1=−a1+n2{c_1} = - a\sqrt {1 + {n^2}} by c2=a1+n2{c_2} = a\sqrt {1 + {n^2}} , we get
⇒c1c2=−a1+n2a1+n2=−1\Rightarrow \dfrac{{{c_1}}}{{{c_2}}} = \dfrac{{ - a\sqrt {1 + {n^2}} }}{{a\sqrt {1 + {n^2}} }} = - 1
Therefore, we can observe that ⇒a1a2=b1b2≠c1c2\Rightarrow \dfrac{{{a_1}}}{{{a_2}}} = \dfrac{{{b_1}}}{{{b_2}}} \ne \dfrac{{{c_1}}}{{{c_2}}}.
Therefore, the lines −nx+y−a1+n2=0 - nx + y - a\sqrt {1 + {n^2}} = 0 and −nx+y+a1+n2=0 - nx + y + a\sqrt {1 + {n^2}} = 0 have no solution.
This means that the lines rr and ss are parallel lines.
We can show this in the form of a diagram.

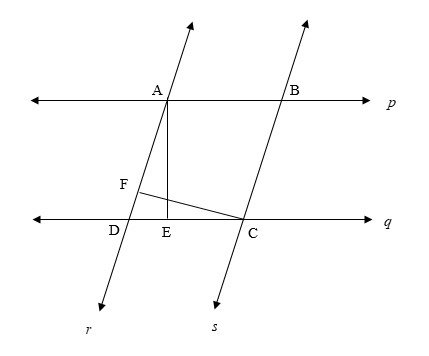
Here, the quadrilateral formed by the 4 lines is a parallelogram, since the opposite pairs of sides are parallel.
Now, we will find the two altitudes of the parallelogram.
The distance between two parallel lines ax+by+c1=0ax + by + {c_1} = 0 and ax+by+c2=0ax + by + {c_2} = 0 is given by the formula d=∣c2−c1∣a2+b2d = \dfrac{{\left| {{c_2} - {c_1}} \right|}}{{\sqrt {{a^2} + {b^2}} }}.
The distance between the parallel lines pp and qq is the altitude AE.
Since the lines pp and qq, that is −mx+y−a1+m2=0 - mx + y - a\sqrt {1 + {m^2}} = 0 and −mx+y+a1+m2=0 - mx + y + a\sqrt {1 + {m^2}} = 0 are parallel lines, we get the distance between them as
AE=∣a1+m2−(−a1+m2)∣(−m)2+12AE = \dfrac{{\left| {a\sqrt {1 + {m^2}} - \left( { - a\sqrt {1 + {m^2}} } \right)} \right|}}{{\sqrt {{{\left( { - m} \right)}^2} + {1^2}} }}
Simplifying the expression, we get
AE=∣a1+m2+a1+m2∣m2+1 ⇒AE=∣a1+m2+a1+m2∣m2+1\begin{array}{l} AE = \dfrac{{\left| {a\sqrt {1 + {m^2}} + a\sqrt {1 + {m^2}} } \right|}}{{\sqrt {{m^2} + 1} }}\\\ \Rightarrow AE = \dfrac{{\left| {a\sqrt {1 + {m^2}} + a\sqrt {1 + {m^2}} } \right|}}{{\sqrt {{m^2} + 1} }}\end{array}
Further simplifying the expression, we get
⇒AE=∣2a1+m2∣m2+1 ⇒AE=∣2a∣ ⇒AE=2a\begin{array}{l} \Rightarrow AE = \dfrac{{\left| {2a\sqrt {1 + {m^2}} } \right|}}{{\sqrt {{m^2} + 1} }}\\\ \Rightarrow AE = \left| {2a} \right|\\\ \Rightarrow AE = 2a\end{array}
The distance between the parallel lines rr and ss is the altitude CF.
Since the lines rr and ss, that is −nx+y−a1+n2=0 - nx + y - a\sqrt {1 + {n^2}} = 0 and −nx+y+a1+n2=0 - nx + y + a\sqrt {1 + {n^2}} = 0 are parallel lines, we get the distance between them as
CF=∣a1+n2−(−a1+n2)∣(−n)2+12CF = \dfrac{{\left| {a\sqrt {1 + {n^2}} - \left( { - a\sqrt {1 + {n^2}} } \right)} \right|}}{{\sqrt {{{\left( { - n} \right)}^2} + {1^2}} }}
Simplifying the expression, we get

\begin{array}{l} CF = \dfrac{{\left| {a\sqrt {1 + {n^2}} + a\sqrt {1 + {n^2}} } \right|}}{{\sqrt {{n^2} + 1} }}\\\ \Rightarrow CF = \dfrac{{\left| {a\sqrt {1 + {n^2}} + a\sqrt {1 + {n^2}} } \right|}}{{\sqrt {{n^2} + 1} }}\\\\\end{array}$$ After simplification on the expression, we get $$ \begin{array}{l} CF = \dfrac{{\left| {2a\sqrt {1 + {n^2}} } \right|}}{{\sqrt {{n^2} + 1} }}\\\ \Rightarrow CF = \left| {2a} \right|\\\ \Rightarrow CF = 2a\end{array}$$ Now, the area of a parallelogram is the product of its base and the altitude on the base. Thus, we get Area of parallelogram ABCD $$ = CD \times AE$$ Also, using the altitude CF, we get Area of parallelogram ABCD $$ = AD \times CF$$ Thus, we get $$CD \times AE = AD \times CF$$ Substituting $$AE = 2a$$ and $$CF = 2a$$ in the equation, we get $$ \Rightarrow CD \times 2a = AD \times 2a$$ Simplifying the expression, we get $$ \Rightarrow CD = AD$$ We know that if any two adjacent sides of a parallelogram are equal, the parallelogram is a rhombus. Therefore, since $$CD = AD$$, we get that ABCD is a rhombus. **Thus, the correct option is option (b).** **Note:** We can also prove that the lines $$p,q$$ and $$r,s$$ are not parallel before drawing the figure, because it can be possible that all the four lines are parallel and no quadrilateral is formed. Comparing line $$p$$, that is $$ - mx + y - a\sqrt {1 + {m^2}} = 0$$ to the standard form $${a_1}x + {b_1}y + {c_1} = 0$$, we get $${a_1} = - m$$, $${b_1} = 1$$, and $${c_1} = - a\sqrt {1 + {m^2}} $$ Comparing line $$s$$, that is $$ - nx + y + a\sqrt {1 + {n^2}} = 0$$ to the standard form $${a_2}x + {b_2}y + {c_2} = 0$$, we get $${a_2} = - n$$, $${b_2} = 1$$, and $${c_2} = a\sqrt {1 + {n^2}} $$ Dividing $${a_1} = - m$$ by $${a_2} = - m$$, we get $$\dfrac{{{a_1}}}{{{a_2}}} = \dfrac{{ - m}}{{ - n}} = \dfrac{m}{n}$$ Dividing $${b_1} = 1$$ by $${b_2} = 1$$, we get $$\dfrac{{{b_1}}}{{{b_2}}} = \dfrac{1}{1} = 1$$ Since $$\dfrac{{{a_1}}}{{{a_2}}} \ne \dfrac{{{b_1}}}{{{b_2}}}$$, we have proved that the lines $$p$$ and $$s$$ have unique solution, and thus are intersecting lines. Since $$p,q$$ are parallel, and $$r,s$$ are parallel, the lines $$p,q$$ are intersecting with lines $$r,s$$. Thus, our drawn figure is correct.