Question

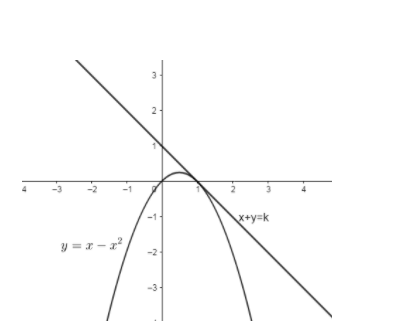
The straight line x + y = k touches the parabola, $y=x-{{x}^{2}}$, if k =
(a) 0
(b) -1
(c) 1
(d) None of these

Answer 1

Hint: First of all write x + y = k as y = k – x. Then, from both equations we can equate y and get a quadratic equation. Since the line touches the parabola, the roots will be equal and so we know that the discriminant of the quadratic equation will be zero. Hence we can substitute and get the value of k.

Complete step-by-step answer:
We have been given the equation of a straight line as x + y = k.
The equation of parabola is $y=x-{{x}^{2}}$. Thus we can say that x + y = k is tangent of parabola, $y=x-{{x}^{2}}$.

Now let us find the point of contact. For that we have to substitute either x or y in terms of y or x respectively and k from the equation of the line in the equation of the parabola.
x + y = k – (1)
$y=x-{{x}^{2}}$- (2)
From (1), we can say that, y = k – x.
Now let us equate both expressions on y.
k – x = $x-{{x}^{2}}$
Let us rearrange the expression,
$\Rightarrow {{x}^{2}}-2x+k=0$ - (3)
Now the above equation is similar to the quadratic equation’s general form, $a{{x}^{2}}+bx+c=0$ - (5).
We have been told that the straight line touches the parabola, then the roots are equal. Thus when roots are equal, the discriminant of quadratic formula will be zero. i.e. D = 0.
Which means that, ${{b}^{2}}-4ac=0$ - (5)
By comparing (3) and (4), we get
a = 1, b = -2 and c = k.
Hence let us put these values in (5).

& {{\left( -2 \right)}^{2}}-4\times 1\times k=0 \\\ & \Rightarrow 4-4k=0 \\\ & \therefore 4=4k \\\ \end{aligned}$$ i.e. we get, $$k=\dfrac{4}{4}=1$$. Thus we got the value of k = 1. $$\therefore $$ Option (c) is the right answer. Note: When a, b and c are real numbers, $$a\ne 0$$ and the discriminant is zero, then the roots of the quadratic equation are real and equal. The discriminant of the resulting quadratic is zero, then the line is tangent to the parabola. One can also think of rearranging the first equation as x = k – y and then substituting in the second equation. This is also possible, but it will complicate the whole solution and will be more time consuming.