Question

The stopping potential for the photoelectron emitted from a mental surface of work function $1.7\;eV$ is $10.4\;eV$. Identify the energy levels corresponding to the transition in hydrogen atom which will result in emission of wavelength equal to that of incident radiation for the atom photoelectric effect.

Answer 1

We know that photoelectric effect is the process observed when the incident radiation of light having energy more than the threshold energy or the work function is incident surface, emits charged particles, called the photons. Using the formula of photoelectric effect we can solve the following questions.

Complete step-by-step solution:
We know from the dual nature of light, that it is both wave and also contains particles or photons. Photoelectric electric effect is a foundation to prove that light has particle nature. As defined above, it was found that light particles are nothing but species called photons. From Planck’s equation, we know the energy $E$ of light as a wave can be expressed as
$E=hv=\dfrac{hc}{\lambda}$, where $h$ is Planck's constant and $v$ denotes the frequency of light waves with speed $c$ and wavelength $\lambda$.
Thus, here in photoelectric effect , when a light with some energy is incident on a metal, the energy of the light $E_p$ wave gets distributed as the energy of the electron $E_e$ and the threshold or the work energy of the metal $\phi$, and can be expressed as
$E_p=E_e+\phi$
Here, given that $\phi=10.4ev$ and $E_e=1.7ev$
Then the energy of the photon $E_p= 10.4+1.7=12.1eV$

Consider the energy level of hydrogen atom as shown below

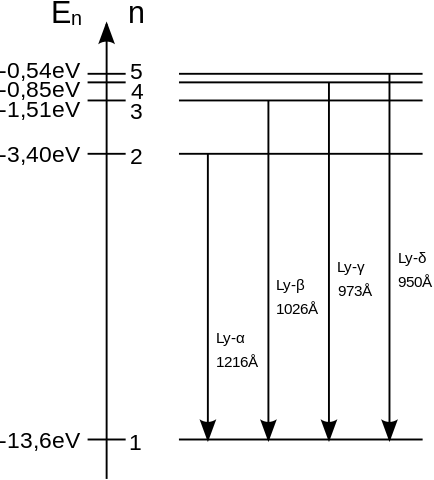
The energy levels, which corresponds to $E_p$ is from $n=3$ to $n=1$ as $E_3-E_1=-1.51+13.6=12.1eV$

Note: Here, we must first calculate the energy of a photon, by photoelectric effect, and then compare the energy obtained to find the energy level of hydrogen. Here, it is important to note that the photon is nothing but the hydrogen atom which is undergoing excitation; hence we must compare the energy of the photon to the difference of the energy levels of the hydrogen.