Question

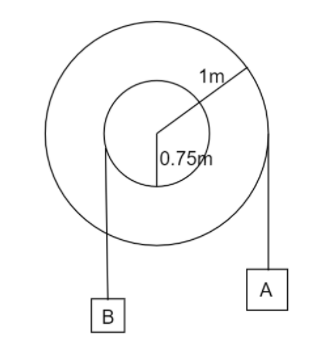
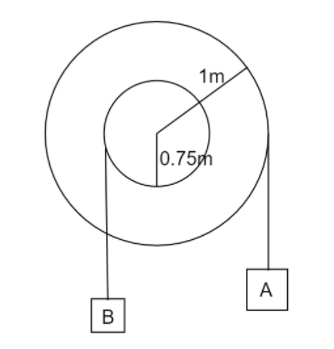
The step pulley shown starts from rest and accelerates at $2$ $rad$ ${s^{ - 2}}$,
What time $t$ is required for block A to move $20m$ ?
A) $4.47s$
B) $3.47s$
C) $5.47s$
D) $6.47s$

Answer 1

A changing angular velocity indicates the presence of an angular acceleration in a rigid body, typically measured in $rad$ ${s^{ - 2}}$. Find the translational acceleration for both blocks A and B. Use the second equation of motion which is $S = ut + \dfrac{1}{2}a{t^2}$ and find the value of $t$.

Complete step by step answer:

Here, the block A moves with an acceleration of ${a_A}$ downwards and the block B moves with an acceleration of ${a_B}$ upwards.
Given is $R = 1m$and $r = 0.75m$
We know, Translational acceleration is given by $a = r\alpha$ where $r$ is the radius from the axis of rotation and $\alpha$ is angular acceleration. The angular acceleration is the rate of change of the angular velocity, just as acceleration is the rate of change of velocity.
So for block A angular acceleration ${a_A} = 2 \times 1 = 2m/{s^2}$
And for block B angular acceleration ${a_B} = 2 \times 0.75 = 1.5m/{s^2}$
Initially, it is starting from rest so $u = 0$
${a_A} = 2m/{s^2}$
For block A to move to a Distance $S = 20m$
Using the second equation of motion
$S = ut + \dfrac{1}{2}a{t^2}$
Putting the values from above
$\Rightarrow 20 = 0 \times t + \dfrac{1}{2} \times 2 \times {t^2}$
$\Rightarrow t = \sqrt {20}$
$\Rightarrow t = 4.47s$
Hence time required by block A to move $20m$ is $4.47s$. So, option (A) is correct.

Note: The translational acceleration of a point on the object rotating is given by $a = r\alpha$ where $r$ is the radius or distance from the axis of rotation. This is also the tangential component of acceleration: it is tangential to the direction of motion of the point. If this component is $0$, the motion is a uniform circular motion, and the velocity changes in direction only.