Question

The standard weight of a special purpose brick is 5 kg and it must contain two basic ingredients ${{B}_{1}}\And {{B}_{2}}$. ${{B}_{1}}$ costs Rs 5 per kg and ${{B}_{2}}$ costs Rs 8 per kg. Strength considerations dictate that the brick should contain not more than 4 kg of ${{B}_{1}}$ and minimum 2 kg of${{B}_{2}}$. Since the demand for the product is likely to be related to the price of the brick, find the minimum cost of brick satisfying the above conditions. Formulate this situation as an L.P.P and solve it graphically.

Answer 1

Let us assume that x kg of ${{B}_{1}}$ is required and y kg of ${{B}_{2}}$ is required. It is given that the standard weight of the brick is 5 kg so addition of x and y is 5. Then apply the conditions on the basic ingredients ${{B}_{1}}\And {{B}_{2}}$ that the brick should contain not more than 4 kg of ${{B}_{1}}$ and minimum 2 kg of ${{B}_{1}}$. After that we have to find the minimum cost of brick so write the cost of brick to be made with the strength considerations which is written by multiplying Rs 5 by x and add this result of multiplication with the multiplication of Rs 8 by y. Draw the conditions on the graph and find the intersecting values and substitute them in the minimum cost expression to get the minimum cost.

Complete step-by-step answer :
Let us assume that the weight of basic ingredients ${{B}_{1}}\And {{B}_{2}}$ in the brick is x kg and y kg respectively.
It is given that the standard weight of the brick is 5 kg so the addition of weight of the basic ingredients ${{B}_{1}}\And {{B}_{2}}$ is equal to 5.
Adding x kg and y kg and equating the addition to 5 we get,
$\left( x+y \right)=5$………… Eq. (1)
Now, there is a condition on the basic ingredients ${{B}_{1}}\And {{B}_{2}}$ that brick should contain not more than 4 kg of ${{B}_{1}}$ and minimum 2 kg of ${{B}_{2}}$ so applying these conditions on x and y we get,
$\begin{aligned} & x\le 4.......Eq.(2) \\\ & y\ge 2........Eq.(3) \\\ \end{aligned}$
It is given that ${{B}_{1}}$ costs Rs 5 per kg and ${{B}_{2}}$ costs Rs 8 per kg so the total cost of the brick is calculated by multiplying x by 5 and add the result of this multiplication to the multiplication of y by 8.
Cost of the brick is equal to:
$5x+8y$
Let us represent the above cost of the brick as “Z”.
$Z=5x+8y$…………. Eq. (4)
We have to minimize the above cost of the brick which we are going to do by finding the intersections of eq. (1, 2 & 3) on the graph paper and the points where substitute the intersecting points in the above expression in Z and see which point is giving the minimum value.

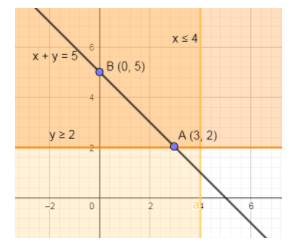
The two points $A\left( 3,2 \right)\And B\left( 0,5 \right)$ in the above diagram are points of intersection of the eq. (1, 2 & 3).
Substituting the point $A\left( 3,2 \right)$ in eq. (4) we get,
$\begin{aligned} & Z=5x+8y \\\ & \Rightarrow Z=5\left( 3 \right)+8\left( 2 \right) \\\ & \Rightarrow Z=15+16 \\\ & \Rightarrow Z=31 \\\ \end{aligned}$
Substituting the point $B\left( 0,5 \right)$ in eq. (4) we get,
$\begin{aligned} & Z=5x+8y \\\ & \Rightarrow Z=5\left( 0 \right)+8\left( 5 \right) \\\ & \Rightarrow Z=0+40 \\\ & \Rightarrow Z=40 \\\ \end{aligned}$
From the above two values, you can see that the minimum value is 31. Hence, the minimum cost of the brick is equal to Rs 31.

Note : The blunder that could happen in the above problem is in writing the inequality in minimum condition. For instance, in the above solution we have given that the minimum weight that ${{B}_{2}}$ can have is 2 kg so you might have thought that in the minimum condition which inequality should be there either $\le$ or $\ge$. The solution to this problem is that it is given that the minimum weight that ${{B}_{2}}$ can have is 2 kg means the ingredient ${{B}_{2}}$ should take values 2 kg or greater than 2 kg so $\ge$ inequality will come for minimum.