Question

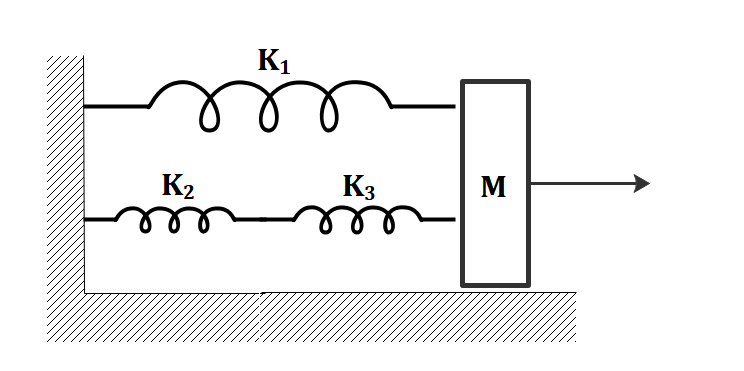
The springs shown in the figure are all unstretched in the beginning when a man starts pulling the block. The man exerts a constant force F on the block. Find the amplitude and the frequency of the motion of the block.

Answer 1

We are given a spring-mass system where the springs of spring constant $K_{2}$ and $K_{3}$ are connected series, and then connected in parallel to the spring of spring constant $K_1$. We need to find the equivalent of the springs, so as to replace the system of springs as one single spring. Once the force F is applied, the block of mass M will start oscillating in SHM. We can find the amplitude from the equation of force in spring. And the frequency from the formula for the time period of the block-spring system in SHM.
Formula used:
\eqalign{ & \dfrac{1}{{{K_P}}} = \dfrac{1}{{{K_1}}} + \dfrac{1}{{{K_2}}} \cr & {K_S} = {K_1} + {K_2} \cr & x = \dfrac{F}{K} \cr & T = 2\pi \sqrt {\dfrac{M}{K}} \cr}

Complete answer:
From the figure given in the question, we can see that the springs with spring constant $K_{2}$ and $K_{3}$ are connected in series. The equivalent of these springs say, $K_{23}$ which are connected in series can be written as
\eqalign{ & \dfrac{1}{{{K_{23}}}} = \dfrac{1}{{{K_2}}} + \dfrac{1}{{{K_3}}} \cr & \Rightarrow \dfrac{1}{{{K_{23}}}} = \dfrac{{{K_3} + {K_2}}}{{{K_2}{K_3}}} \cr & \Rightarrow {K_{23}} = \dfrac{{{K_2}{K_3}}}{{{K_3} + {K_2}}} \cr}
Now, both these springs are connected in parallel to the spring with spring constant $K_1$. Say, the equivalent of all these springs is Keq. Then this Keq is given by
\eqalign{ & {K_{eq}} = {K_1} + {K_{23}} \cr & \Rightarrow {K_{eq}} = {K_1} + \dfrac{{{K_2}{K_3}}}{{{K_3} + {K_2}}} \cr & \Rightarrow {K_{eq}} = \dfrac{{{K_1}{K_3} + {K_1}{K_2} + {K_2}{K_3}}}{{{K_3} + {K_2}}} \cr}
So, from this, the three springs can be replaced by a single spring with spring constant Keq.
It is said that a man applies a force F on the mass M. Then the block will start to oscillate in SHM. The amplitude or the maximum displacement is given by
\eqalign{ & F = {K_{eq}}x \cr & \Rightarrow x = \dfrac{F}{{{K_{eq}}}} \cr & \Rightarrow x = \dfrac{F}{{\dfrac{{{K_1}{K_3} + {K_1}{K_2} + {K_2}{K_3}}}{{{K_3} + {K_2}}}}} \cr & \Rightarrow x = \dfrac{{F\left( {{K_3} + {K_2}} \right)}}{{{K_1}{K_3} + {K_1}{K_2} + {K_2}{K_3}}} \cr}
Therefore, the amplitude of the block is $\dfrac{{F\left( {{K_3} + {K_2}} \right)}}{{{K_1}{K_3} + {K_1}{K_2} + {K_2}{K_3}}}$.
The time period of this SHM is given by
$T = 2\pi \sqrt {\dfrac{M}{K}}$
Where,
T is the time period of oscillation;
M is the mass attached to the spring; and
K is the spring constant.
Here, the mass is also given as M and the spring constant will be Keq. Substituting these quantities in the formula, we have
\eqalign{ & T = 2\pi \sqrt {\dfrac{M}{K}} \cr & \Rightarrow T = 2\pi \sqrt {\dfrac{M}{{{K_{eq}}}}} \cr & \Rightarrow T = 2\pi \sqrt {\dfrac{{M\left( {{K_1}{K_3} + {K_1}{K_2} + {K_2}{K_3}} \right)}}{{{K_3} + {K_2}}}} \cr}
The frequency, say, f of the oscillation will be the reciprocal of the time period, i.e.
\eqalign{ & f = \dfrac{1}{T} \cr & \Rightarrow f = \dfrac{1}{{2\pi \sqrt {\dfrac{{M\left( {{K_1}{K_3} + {K_1}{K_2} + {K_2}{K_3}} \right)}}{{{K_3} + {K_2}}}} }} \cr & \Rightarrow f = \dfrac{1}{{2\pi }}\sqrt {\dfrac{{{K_3} + {K_2}}}{{M\left( {{K_1}{K_3} + {K_1}{K_2} + {K_2}{K_3}} \right)}}} \cr}
Therefore, the frequency of the spring is given by $\dfrac{1}{{2\pi }}\sqrt {\dfrac{{{K_3} + {K_2}}}{{M\left( {{K_1}{K_3} + {K_1}{K_2} + {K_2}{K_3}} \right)}}}$.

Note:
If you are either confused or couldn’t remember the equivalent of springs connected in series and parallel, you can simply derive them by remembering small conditions. For any springs connected in series, the total elongation in spring will be the sum of elongation in each spring. For springs in parallel, the elongation will be the same in each spring.