Question
Question: The springs in figure A and B are identical but the length of spring in A is three times than the le...
The springs in figure A and B are identical but the length of spring in A is three times than the length of each spring in B. The ratio of period TBTA:
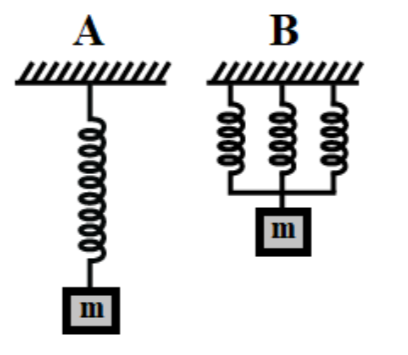
A. 3B. 31C. 3D. 31
Solution
For a simple spring-mass system, we can apply the direct equation to obtain the time period of the simple harmonic motion executed by the system. When springs are connected in parallel combination, the displacement of each spring is the same, but the restoring force is different. In a parallel combination system, we need to calculate the equivalent spring constant of the combination and thus the time period of the simple harmonic motion executed by the system.
Complete step-by-step solution:
A vertical spring-mass system undergoes simple harmonic motion in the vertical direction about the mean or equilibrium position. The equilibrium position in a spring system is the point where the net force acting on the mass is zero.
Spring mass system can be composed of different combinations, series combinations and parallel combinations.
1). When springs are connected in series combination, the force acting on each string is the same, but the displacement of each string is different.
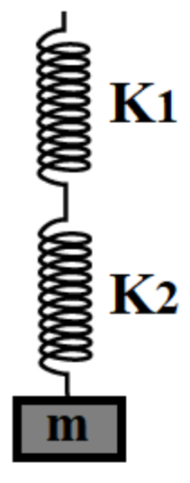
The equivalent spring constant in a series combination of spring system is given as,
KS=K1+K2K1K2
The time period in the series combination of spring system is given as,
T=2πK1+K2K1K2m⇒T=2πK1K2m(K1+K2)
2). When springs are connected in parallel combination, the displacement of each spring is the same, but the restoring force is different.
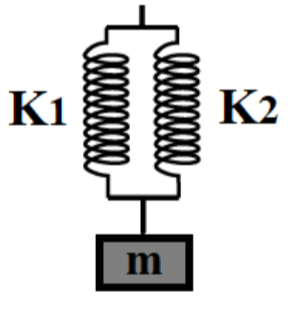
The equivalent spring constant in parallel combination of spring system is given as,
KP=K1+K2
The time period in series combination of spring system is given as,
T=2πK1+K2m
We are given that the two springs A and B are identical but the length of spring in A is three times than the length of each spring in B. The ratio of period TBTA:
The spring constant is inversely proportional to the length of the spring, that is,
K∝L1
Where,
K is the spring constant and,
L is the length of the spring
Let the spring constant of A is KA and the spring constant of each spring in B is KB
Let the length of spring A is LA and the length of each spring B is LB
Given that,
LA=3LB
It means that,
KA=3KB
Or,
KB=3KA
The equivalent spring constant in B is given as,
KeqB=KB+KB+KB=3KB
Put KB=3KA
We get,
KeqB=9KA
(Let’s say equation 1)
The time period of spring system A is given as,
TA=2πKAm
(Let’s say equation 2)
Where,
m is the mass attached to the spring
KA is the spring constant of A
The time period of spring system B is given as,
TB=2πKeqBm
(Let’s say equation 3)
Where,
m is the mass attached to the spring
KeqB is the equivalent spring constant of B
From equation 1, we have,
KeqB=9KA
It means that,
TB=2π9KAm
(Let’s say equation 4)
Dividing equation 2 and equation 4, we get,
