Question
Question: The spring block system as shown in the figure is in equilibrium. The string connecting blocks A and...
The spring block system as shown in the figure is in equilibrium. The string connecting blocks A and B is cut. The mass of all the three blocks is m and the spring constant of both the springs is k. The amplitude of resulting oscillation of block A is :
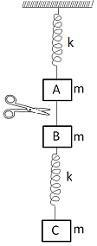
Solution
Hint: Here in this question we will use the Hooke’s law i.e. mg+mg+mg=kx and we will draw a diagram by identifying the part of the spring block system .
Formula used: mg+mg+mg=kx
Complete step-by-step answer:
Here , let x is the extension of spring just after cutting.
Applying Hooke’s law , mg+mg+mg=kx,x=k3mg
The spring extension, when block A is in the mean position
=kmg
Amplitude of oscillation of A
=k3mg−kmg=k2mg
Note: Hooke’s law in physics states that the force required to extinguish or compress a spring linearly with respect to F8=kx distance, where k is characteristic of the spring constant factor. In many other situations where an elastic body is deformed. Hooke 's equation holds such as wind blowing on a tall building, and a musician plucking a guitar string. An elastic body or material; this equation is said to be linear elastic or hookean for which one would presume.
