Question

The ‘spin only’ magnetic moment of $N{i^{2 + }}$ in aqueous solution would be:
A. $\sqrt 6 BM$
B. $\sqrt {15} BM$
C. $\sqrt 2 BM$
D. $\sqrt 8 BM$

Answer 1

The net magnetic moment of an atom/ion is the vector sum of its orbital and spin magnetic moments. We can easily calculate the spin only magnetic moment using the formula ${u_{spin}} = \sqrt {n(n + 2)}$ where n is the number of unpaired electrons present in an atom or ion. Bohr magneton or BM is the unit of magnetic moment.

Complete step by step answer:
$Ni$ is present in $N{i^{2 + }}$ oxidation state as ${\left[ {Ni{{({H_2}O)}_6}} \right]^{2 + }}$
First of all, we know that Ni is a d-block element and ${H_2}O$ being an electron rich species (due to presence of two lone pairs on oxygen atoms) can easily form a coordinate compound.
We look, into the electronic configuration of $N{i^{2 + }}$ ion ${\left[ {Ni{{({H_2}O)}_6}} \right]^{2 + }}$
$Ni = {16^2}2{s^2}2{p^6}3{s^2}3{p^6}3{d^8}4{s^0}$
$N{i^{2 + }} = 1{s^2}2{s^2}2{p^6}3{s^2}3{p^6}3{d^8}4{s^0}$
Thus, according to valence and theory (VB+) water being a ligand form of a high spin complex with $N{i^{2 + }}$ and this can be as show below

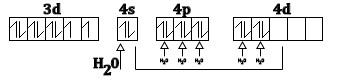
The electrons are filled according to Hund’s rule. Thus, the spin only magnetic moment can be easily calculated using the data given above. As we have seen there are two unpaired electrons in the complex compound so
${u_{spin}} = \sqrt {n(n + 2)} \,BM$
$= \,\sqrt {2(2 + 2)} \,BM$
$= \,\sqrt 8 \,BM$
Where, BM= Bohr magneton
Hence, option (d) is the correct option.

Note:
Student can also use an alternative method to calculate the spin only magnetic moment of the atom or ion by using a formula
${u_{spin}} = \,\sqrt {4s(s + 1)} \,BM$
Where, s= angular spin moment quantum number.
For $N{i^{2 + }}$ with two unpaired electrons
$s = \dfrac{1}{2} + \dfrac{1}{2} = 1$
Therefore, ${u_{spin}} = \sqrt {4 \times 1(1 + 1)} \,BM$
$\Rightarrow \,\sqrt 8 \,BM$ which is the required solution.