Question

The speed-time graph of a particle moving along a fixed direction is shown in the figure. The distance traversed by the particle between t = 2 s the particle t = 6 s is

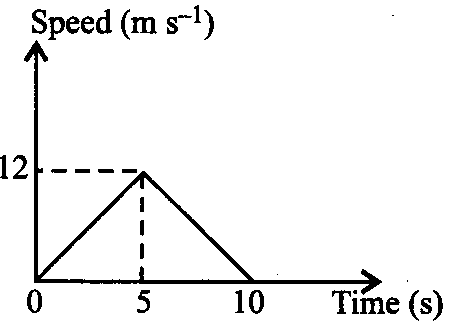
• A. 26 m
• B. 36 m
• C. 46 m
• D. 56 m

Answer 1

Answer: (B)

36 m

Answer 2

Let $S_{1}$ be the distances travelled by particle in time 2 to 5 s and $S_{2}$be the distance travelled by particle in time 5 to 6s.

$\therefore$Total distance travelled, S= $S_{1} + S_{2}.$

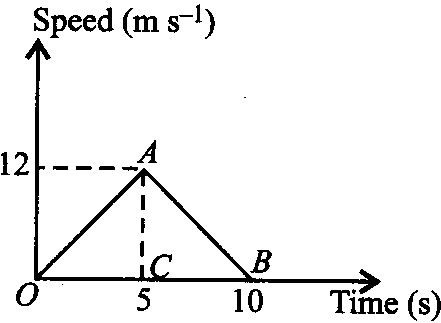
During the time interval 0 to 5s, the accelerations of particle is equal to the slope of line OA.

i.e., $a = \frac{12}{5} = 2.4ms^{- 2}$

Velocity at the end of 2s will be.

V = 0 + $2.4 \times 2 = 4.8ms^{- 1}$

Taking motion of particle for time interval 2s to 5s,

Here, u = $4.8ms^{- 1},a = 2.4ms^{- 2},$

$S = S_{1},t = 5 - 2 = 3s$

Then. $S_{1} = 4.8 \times 3 + \frac{1}{2} \times 2.4 \times 3^{2} = 25.2m$

Accelerations of the particle during the motion t = 5 s to t = 10s is

A = Slope of line AB = $- \frac{12}{5} = - 2.4ms^{- 2}$

Taking motions of the particle for the time 1s (i.e. 5s to 6s),

Here, u = 12m $s^{- 1}$,a =- $2.4ms^{- 2},$ t = 1s , $S = S_{2}$

$\therefore$ $S_{2} = 12 \times 1 + \frac{1}{2}( - 2.4) \times 1^{2} = 10.8m$

$\therefore$ $S = S_{1} = 25.2 + 10.8 = 36m$