Question: The speed of sound in air is 333m/s. The fundamental frequency of the open pipe is 333Hz. The second...

Question

The speed of sound in air is 333m/s. The fundamental frequency of the open pipe is 333Hz. The second overtone of the open organ pipe can be produced with a pipe of length:
A. 0.5 m
B. 1.0 m
C. 1.5 m
D. 2.0 m

Answer 1

Solution

Condition for production of standing waves is to be used here. Second overtone in an open pipe corresponds to a frequency that is around thrice the fundamental frequency. There are around three peaks of a wave that fit into the pipe in such a case.

Formula used:
The formula for the length of the pipe is:
$L = \dfrac{nv}{2 \nu}$
Where n= 1 for fundamental frequency and n= 3 for second overtone.

Complete answer:

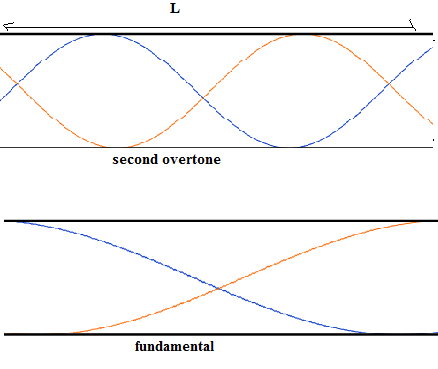
In an open pipe, for fundamental frequency, to produce standing wave we require that the length of the pipe should be twice the wavelength of the fundamental mode or:
$\dfrac{\lambda}{2} = L$
The relation with frequency is:
$L = \dfrac{v}{2 \nu}$
where v is the velocity of sound in our case.
This is so because frequency and wavelength are related as:
$v=\nu \lambda$
For the second overtone, the wavelength is thrice of fundamental wavelength. Therefore, we replace $\lambda$ by $3 \times \lambda$

Keeping this in the formula for length and keeping the velocity of sound 333 m/s (given) in place of v:

$L = \dfrac{999 m/s}{2 \times 333 Hz}$
$L = \dfrac{ 3}{2}$ m
L= 1.5 m

Therefore, the correct option is 1.5 m.

So, the correct answer is “Option C”.

Additional Information:
Standing waves result as a superposition of incoming waves and outgoing waves such that their phases become opposite. The best method to remember standing wave condition is to think of a rope with its one end tied. When we create a wave in such rope, at the tied end the wave reverses back and comes to us. Therefore, the entire rope seems to be making simple up and down motion.

Note:
The unit of frequency Hz is also $s^{-1}$ that is how we got cancellation of this in numerator and denominator and only m remained. Also the frequency and wavelength relation might get confusing. To sort it out, refer to the diagram; 3 times the new wavelength is twice the pipe length.