Question

The speed of Earth’s rotation about its axis is $\varpi$ . Its speed is increased to $x$ times to make the effective acceleration due to gravity equal to zero at the equator, then $x$ is around ($g=10m{{s}^{-2}},R=6400km$)
A. $1$
B. $8.5$
C. $17$
D. $34$

Answer 1

Here we will clear our concept related to variation of gravitational force in difference in latitude. We will know which force will be acting on Earth. Earth is under the influence of centripetal and centrifugal force as it rotates on its own axis.

Complete answer:
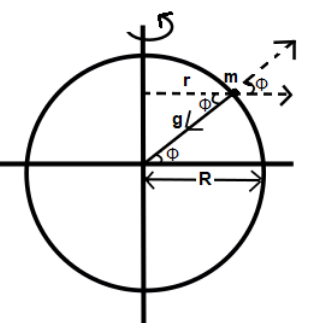
The centripetal and centrifugal force come in picture when an object is in circular motion and so is our Earth. Let us consider a body of mass $m$ at the latitude, which makes an angle $\phi$ at the center of the Earth. Now, as Earth rotates on its axis, then mass m will also rotate and form a circle about the axis of rotation.

And, as the body rotates in a circular motion then, there is a centrifugal force which acts outside away from the center of the circle. Hence the effective gravity will be $g'=g-{{\varpi }^{2}}R{{\cos }^{2}}\phi$. When the body is at equator, $\cos \phi =\cos 0=1$ thus the net acceleration will be $g'=g-{{\varpi }^{2}}R$

We know that Earth takes 24 hours to rotate about its own axis. So,
$T=24\times 60\times 60\,s$
Angular speed of Earth about its own axis will be:
$\varpi =\dfrac{2\pi }{T}=\dfrac{2\pi }{24\times 60\times 60}rad{{s}^{-1}}$
At equator, $g'=g-{{R}_{e}}^{2}g'=g-{{R}_{e}}\varpi {{'}^{2}}$ or $0=g-{{R}_{e}}\varpi {{'}^{2}}$
So, $\varpi '=\sqrt{\dfrac{g}{{{R}_{e}}}}=\dfrac{2\pi }{84.6\times 60}$
When we take their ratio we get
$\dfrac{\varpi '}{\varpi }=\dfrac{24\times 60\times 60}{84.6\times 60}\approx 17$
$\therefore \varpi '=17\varpi$

Hence, the correct answer is option C.

Note: One must know that when the body is placed at pole the angle between center of Earth and the body will be $\phi =90{}^\circ$ $\Rightarrow \cos \phi =\cos 90=0$, therefore the effective gravity will be $g'=g$. Hence, we have the maximum gravitational acceleration at the poles and minimum at the equator.