Question

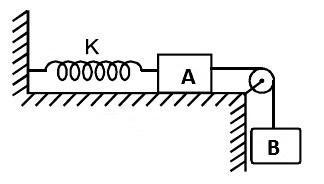
The speed of block A when the extension in the spring is, $x=\dfrac{{{x}_{m}}}{2}$, where ${{x}_{m}}$ is the maximum extension in spring. (Mass of block A is ‘m’ and mass of block B is ‘2m’ and ‘K’ is the spring constant.)

$\begin{aligned} & (A)2g\sqrt{\dfrac{m}{K}} \\\ & (B)2g\sqrt{\dfrac{m}{2K}} \\\ & (C)2g\sqrt{\dfrac{m}{3K}} \\\ & (D)2g\sqrt{\dfrac{m}{4K}} \\\ \end{aligned}$

Answer 1

Firstly, at the condition of maximum extension all the gravitational potential energy will be converted into elastic potential energy of the spring. We will use this relation to find the maximum extension in spring. Once we get this, we will again apply conservation of energy at half the maximum extension to get the velocity of both the blocks.

Complete step-by-step answer:
At the instant of maximum of maximum extension, the decrease in gravitational potential energy of block B will be equal to increase in elastic potential energy of spring. Mathematically, this is:
$\begin{aligned} & \Rightarrow {{m}_{B}}g{{x}_{m}}=\dfrac{1}{2}K{{x}_{m}}^{2} \\\ & \therefore {{x}_{m}}=\dfrac{4mg}{K} \\\ \end{aligned}$
Now, at half the maximum extension (say x), we can write:
$\begin{aligned} & \Rightarrow x=\dfrac{{{x}_{m}}}{2} \\\ & \therefore x=\dfrac{2mg}{K} \\\ \end{aligned}$
Since, both the blocks A and B are connected through string, they velocities will always remain equal. Let the velocity of block A and B be ‘v’.
At half the maximum extension, we can say, the decrease in gravitational potential energy is equal to the increase in elastic potential energy of the spring and the increase in kinetic energy of the two blocks. Mathematically, this can be written as:
$\Rightarrow {{m}_{B}}gx=\dfrac{1}{2}K{{x}^{2}}+\dfrac{1}{2}({{m}_{A}}+{{m}_{B}}){{v}^{2}}$
Putting the values of all the known terms in the above equation, we get:
$\begin{aligned} & \Rightarrow 2mg\left( \dfrac{2mg}{K} \right)=\dfrac{1}{2}K{{\left( \dfrac{2mg}{K} \right)}^{2}}+\dfrac{1}{2}(m+2m){{v}^{2}} \\\ & \Rightarrow \dfrac{4{{m}^{2}}{{g}^{2}}}{K}=\dfrac{2{{m}^{2}}{{g}^{2}}}{K}+\dfrac{3}{2}m{{v}^{2}} \\\ & \Rightarrow \dfrac{2{{m}^{2}}{{g}^{2}}}{K}=\dfrac{3}{2}m{{v}^{2}} \\\ & \Rightarrow v=\sqrt{\dfrac{4m{{g}^{2}}}{3K}} \\\ & \therefore v=2g\sqrt{\dfrac{m}{3K}} \\\ \end{aligned}$
Hence, the velocity of the two blocks A and B comes out to be $2g\sqrt{\dfrac{m}{3K}}$.

So, the correct answer is “Option C”.

Note: We can easily apply conservation of energy at the two instants because, there has been no mention of friction on the blocks due to the surface in contact which can result in loss of energy. When, there is no mention of friction, we shall assume it to be absent and proceed without it in our solution.