Solveeit Logo
Login

Question

Question: The speed of an aircraft in still air is \(200\,km\,{h^{ - 1}}\). The wind blows from the west at a ...

The speed of an aircraft in still air is 200 km h−1200\,km\,{h^{ - 1}}. The wind blows from the west at a speed of 85.0 km h−185.0\,km\,{h^{ - 1}}.
In which direction must the pilot steer the aircraft in order to fly due north?
A) 23.0∘23.0^\circ east of north.
B) 23.0∘23.0^\circ west of north.
C) 25.2∘25.2^\circ east of north.
D) 25.2∘25.2^\circ west of north.

Explanation

Solution

Just keep in mind that the speed of an object in still air is equal to the speed relative to the air, no matter whether the air is moving or not relative to the ground. Also, to get in the north direction all the resultant of all the vectors should be in the north direction.

Complete Step by Step answer
As given in the question, the wind is blowing from the west at a speed of 85 km h−185\,km\,{h^{ - 1}}. The blowing wind will cause the aircraft to change its direction during its motion. Thus, if the pilot wants to steer in the north. Also, the resultant of all the vectors should be in the north direction.
Now, let us represent the velocity of air and wind in the form of a diagram as given below

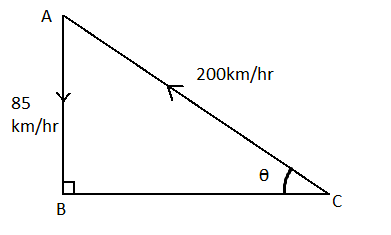
Now, we will calculate the angle subtended by the velocity of air and velocity of aircraft. For this, we are given that,
The Speed of an aircraft, vaircraft=200 km h−1{v_{aircraft}} = 200\,km\,{h^{ - 1}}
Also, the speed of the wind, vwind=85.0 km h−1{v_{wind}} = 85.0\,km\,{h^{ - 1}}
Therefore, the angle subtended θ\theta can be calculated as
sin⁡θ=vaircraftvwind\sin \theta = \dfrac{{{v_{aircraft}}}}{{{v_{wind}}}}
Therefore, putting the values, we get
sin⁡θ=85.0200\sin \theta = \dfrac{{85.0}}{{200}}
⇒θ=sin⁡−185.0200\Rightarrow \theta = {\sin ^{ - 1}}\dfrac{{85.0}}{{200}}
⇒θ=25.2∘\Rightarrow \theta = 25.2^\circ
Therefore, the pilot should steer the aircraft in 25.2∘25.2^\circ west to the north direction so that its resultant direction would be north when the wind blows in the west direction.

Therefore, option (D) is the correct option.

Note: We cannot use the Pythagoras theorem here to calculate the resultant vectors because the velocity of the plane and wind cannot be perpendicular to each other. Also, the magnitude of the resultant is not required to calculate the angle subtended.