Question

The speed of a projectile at its highest point is ${{v}_{1}}$ and at the point half the maximum height is ${{v}_{2}}$. If $\dfrac{{{v}_{1}}}{{{v}_{2}}}=\sqrt{\dfrac{2}{5}}$ then find the angle of projection.
A. $45{}^\circ$
B. $30{}^\circ$
C. $37{}^\circ$
D.$60{}^\circ$

Answer 1

As a first step, you could make a rough diagram of the projectile motion under discussion. Then, you could consider the motion part by part. You could apply Newton’s equation of motion for the case of motion from 0 to H and H to$\dfrac{H}{2}$ separately. Now using those relations along with the given conditions we will get the angle of the projectile.
Formula used:
Equation of motion,
${{v}^{2}}-{{u}^{2}}=2as$

Complete answer:
In the question, we are given the speed of a projectile at the highest point as ${{v}_{1}}$ and at the point that is half the maximum height be${{v}_{2}}$. We are given that,
$\dfrac{{{v}_{1}}}{{{v}_{2}}}=\sqrt{\dfrac{2}{5}}$…………………………………………. (1)
We are supposed to find the angle of projection.

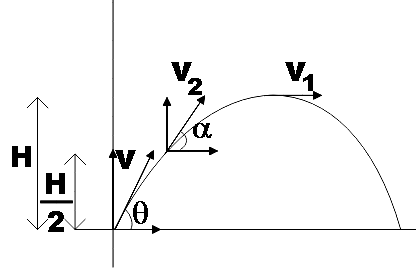
We know that at the highest point the vertical component of velocity is zero. Also, for a projectile motion, the horizontal component of velocity remains the same, that is,
$v\cos \theta ={{v}_{2}}\cos \alpha ={{v}_{1}}$
$\Rightarrow \dfrac{{{v}_{1}}}{{{v}_{2}}}=\cos \alpha =\sqrt{\dfrac{2}{5}}$ ………………………………………. (2)
Now, we could consider the motion from$\dfrac{H}{2}$ to $H$,
Let us recall the Newton’s equation of motion,
${{v}^{2}}-{{u}^{2}}=2as$
$\Rightarrow {{v}_{1y}}^{2}-{{v}_{2y}}^{2}=2{{a}_{y}}s$
$\Rightarrow 0-\left( {{v}_{2}}^{2}{{\sin }^{2}}\alpha \right)=2\left( -g \right)\dfrac{H}{2}$
$\Rightarrow {{v}_{2}}^{2}\left( 1-{{\cos }^{2}}\alpha \right)=gH$
From (2),
$\Rightarrow {{v}_{2}}^{2}\left( 1-\dfrac{2}{5} \right)=gH$
$\therefore {{v}_{2}}=\sqrt{\dfrac{5}{3}}gH$ ……………………………………….. (3)
Now from (1),
$\dfrac{{{v}_{1}}}{{{v}_{2}}}=\sqrt{\dfrac{2}{5}}$
$\Rightarrow {{v}_{1}}={{v}_{2}}\times \sqrt{\dfrac{2}{5}}$
$\Rightarrow {{v}_{1}}=\sqrt{\dfrac{5}{3}}gH\times \sqrt{\dfrac{2}{5}}$
$\therefore {{v}_{1}}=\sqrt{\dfrac{2}{3}}gH$
Similarly, for the motion from 0 to H, we have,
${{v}_{{{1}_{y}}}}^{2}-{{\left( v\sin \theta \right)}^{2}}=2\left( -g \right)H$
$\Rightarrow {{v}^{2}}{{\sin }^{2}}\theta =2gH$
$\Rightarrow \dfrac{{{v}_{1}}^{2}}{{{\cos }^{2}}\theta }{{\sin }^{2}}\theta =2gH$
$\dfrac{2}{3}gH{{\tan }^{2}}\theta =2gH$
$\Rightarrow {{\tan }^{2}}\theta =3$
$\Rightarrow \tan \theta =\sqrt{3}$
$\therefore \theta =60{}^\circ$
Therefore, we found that the angle of the projectile in the given question is found to be $60{}^\circ$ .

Hence, option D is found to be the correct answer.

Note:
We have assigned negative signs for the acceleration of the projectile, because we have chosen the convention in such a way. For questions like this you could consider the motion related to each point mentioned in the question. Doing so, you will easily solve the problem and also avoid confusions.