Question
Question: The speed of a car as a function of time is shown in the figure. Find the distance travelled by the ...
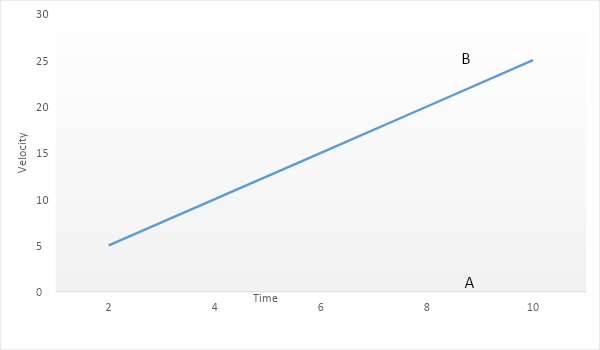
The speed of a car as a function of time is shown in the figure. Find the distance travelled by the car in 8 seconds and its acceleration.
Solution
Hint
To find out the distance travelled by the car and its acceleration, we need to know about the relations between the velocity, acceleration and distance of the car. Velocity is equal to the displacement of the car in a particular given time. In this question, speed and velocity of the car is the same as the distance and displacement is the same.
⇒a=dtdv
And, S=ut+21at2
Where, S is the distance travelled by the car, u is the initial velocity, t is the time taken for covering the distance S, and a is the acceleration of the car.
Complete step by step answer
As we know, the velocity/speed of the car is given by,
⇒v=td
Now, the acceleration is given by the velocity of the car per unit time. This can be written as,
⇒a=tv
In differential form,
⇒a=dtdv
Which is also equal to the slope of the graph.
Thus,
⇒a=dtdv=slope=OAAB
⇒OAAB=820
So, the acceleration of the car is,
⇒a=25=2.5m/s2
Now, we have to find out the distance using one of the equations of motion. It comes as,
⇒S=ut+21at2
Where, S is the distance travelled by the car, u is the initial velocity, t is the time taken for covering the distance S, and a is the acceleration of the car.
By substituting the values in the above equation,
⇒S=0×t+21×2.5×(8)2 ….. (∵ u is the initial velocity of the car and is 0, t=8, a=2.5)
⇒S=80m
Hence, the distance travelled by the car in 8 seconds is 80m and its acceleration is 2.5m/s2.
Note
We can also find out the distance travelled by the car using an alternative method. We know that the area under the v-t graph gives distance, as the displacement as a function of t gives velocity.
Then, the area under the triangle OAB =21×base×height ⇒21×8×20
Thus, we get the distance travelled as 80m from this method also.
