Question
Question: The solution set of the inequality $\frac{|x+2|-|x|}{\sqrt{4-x^3}}\ge 0$ is...
The solution set of the inequality 4−x3∣x+2∣−∣x∣≥0 is
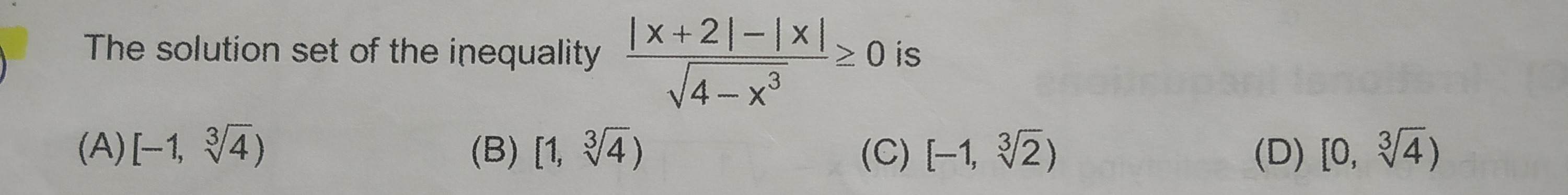
[-1, 34)
[1, 34)
[-1, 32)
[0, 34)
[-1, 34)
Solution
The inequality is given by 4−x3∣x+2∣−∣x∣≥0.
For the expression to be defined, the term under the square root must be non-negative, and the denominator must be non-zero.
So, 4−x3>0, which implies x3<4. Taking the cube root of both sides, we get x<34.
Thus, the domain of the inequality is x∈(−∞,34).
For the inequality 4−x3∣x+2∣−∣x∣≥0 to hold, since the denominator 4−x3 is strictly positive for x<34, the numerator must be non-negative.
So, we need to solve ∣x+2∣−∣x∣≥0 under the condition x<34.
The inequality ∣x+2∣≥∣x∣ can be solved by squaring both sides (since both sides are non-negative):
(x+2)2≥x2
x2+4x+4≥x2
4x+4≥0
4x≥−4
x≥−1.
So, we need to find the values of x that satisfy both x≥−1 and x<34.
The intersection of these two conditions is [−1,34).
