Question
Question: The solution set of $(\frac{2}{3})^{x^{2}-5x+9} > (\frac{27}{8})^{-1}$ is...
The solution set of (32)x2−5x+9>(827)−1 is
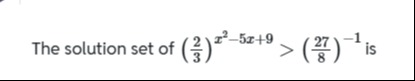
(2,3)
Solution
The given inequality is: (32)x2−5x+9>(827)−1
First, simplify the right-hand side of the inequality: (827)−1=(2333)−1=((23)3)−1 Using the property (am)n=amn and a−1=a1: ((23)3)−1=(23)−3 To match the base on the left-hand side, we can write 23 as (32)−1: (23)−3=((32)−1)−3=(32)(−1)×(−3)=(32)3
Now, substitute this back into the original inequality: (32)x2−5x+9>(32)3
The base of the exponential function is 32. Since 0<32<1, the exponential function f(t)=(32)t is a strictly decreasing function. Therefore, when comparing the exponents, the inequality sign must be reversed: x2−5x+9<3
Now, solve this quadratic inequality: x2−5x+9−3<0 x2−5x+6<0
To find the values of x for which this inequality holds, we first find the roots of the corresponding quadratic equation x2−5x+6=0. We can factor the quadratic expression: (x−2)(x−3)=0 The roots are x=2 and x=3.
Since the coefficient of x2 is positive (which is 1), the parabola y=x2−5x+6 opens upwards. For x2−5x+6<0, the parabola must be below the x-axis. This occurs between its roots. Therefore, the solution for the inequality x2−5x+6<0 is 2<x<3.
The solution set is the open interval (2,3).
