Question
Question: The solution of the equation <img src="https://cdn.pureessence.tech/canvas_87.png?top_left_x=0&top_l...
The solution of the equation  =(1+a)(1+a2)(1+a4) is given by x is equal to.
=(1+a)(1+a2)(1+a4) is given by x is equal to.
A
3
B
5
C
7
D
None of these
Answer
7
Explanation
Solution
We have
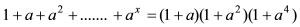
⇒ (1−a)(1−ax+1)=(1+a)(1+a2)+(1+a4)
⇒ (1−ax+1)=(1−a)(1+a)(1+a2)(1+a4)
⇒ (1−ax+1)=(1−a8) ⇒ x+1=8 ⇒ x=7.
