Question

The solution of the equation $4 \cos^2 x + 6 \sin^2 x = 5$ are -

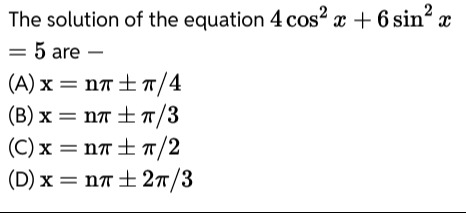
• A. x = $n\pi \pm \pi/4$
• B. x = $n\pi \pm \pi/3$
• C. x = $n\pi \pm \pi/2$
• D. x = $n\pi \pm 2\pi/3$

Answer 1

Answer: (A)

x = $n\pi \pm \pi/4$

Answer 2

The given equation is $4 \cos^2 x + 6 \sin^2 x = 5$. Using the identity $\sin^2 x = 1 - \cos^2 x$, we get: $4 \cos^2 x + 6(1 - \cos^2 x) = 5$ $4 \cos^2 x + 6 - 6 \cos^2 x = 5$ $-2 \cos^2 x = -1$ $\cos^2 x = \frac{1}{2}$ The general solution for $\cos^2 x = \cos^2 \alpha$ is $x = n\pi \pm \alpha$. Since $\cos^2(\frac{\pi}{4}) = \frac{1}{2}$, we have $\alpha = \frac{\pi}{4}$. Therefore, the general solution is $x = n\pi \pm \frac{\pi}{4}$.