Question
Question: The solution of the differential equation $(x + 1) \frac{dy}{dx} - y = e^{3x} (x + 1)^2$ is...
The solution of the differential equation (x+1)dxdy−y=e3x(x+1)2 is
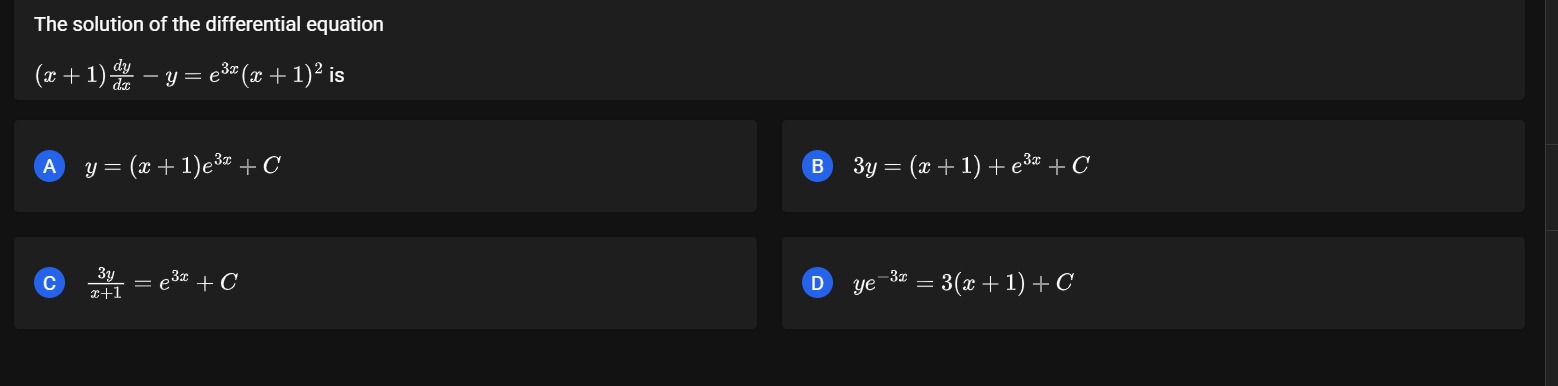
y = (x + 1)e^{3x} + C
3y = (x + 1) + e^{3x} + C
\frac{3y}{x+1} = e^{3x} + C
ye^{-3x} = 3(x + 1) + C
\frac{3y}{x+1} = e^{3x} + C
Solution
The given differential equation is (x+1)dxdy−y=e3x(x+1)2. This is a first-order linear differential equation. We rewrite it in the standard form: dxdy+P(x)y=Q(x).
Divide the entire equation by (x+1): dxdy−x+11y=e3x(x+1)
Comparing with the standard form: P(x)=−x+11 Q(x)=e3x(x+1)
The integrating factor (IF) is IF=e∫P(x)dx. IF=e∫−x+11dx=e−ln∣x+1∣=x+11.
The general solution is y×IF=∫Q(x)×IFdx+C. y×x+11=∫e3x(x+1)×x+11dx+C x+1y=∫e3xdx+C ∫e3xdx=3e3x
So, the solution is: x+1y=3e3x+Cinitial Multiply both sides by 3: x+13y=e3x+3Cinitial Let C=3Cinitial. Thus, the general solution is: x+13y=e3x+C
