Question
Question: The solution of the differential equation $\frac{dy}{dx} = \tan(\frac{y}{x}) + (\frac{y}{x})$ is...
The solution of the differential equation dxdy=tan(xy)+(xy) is
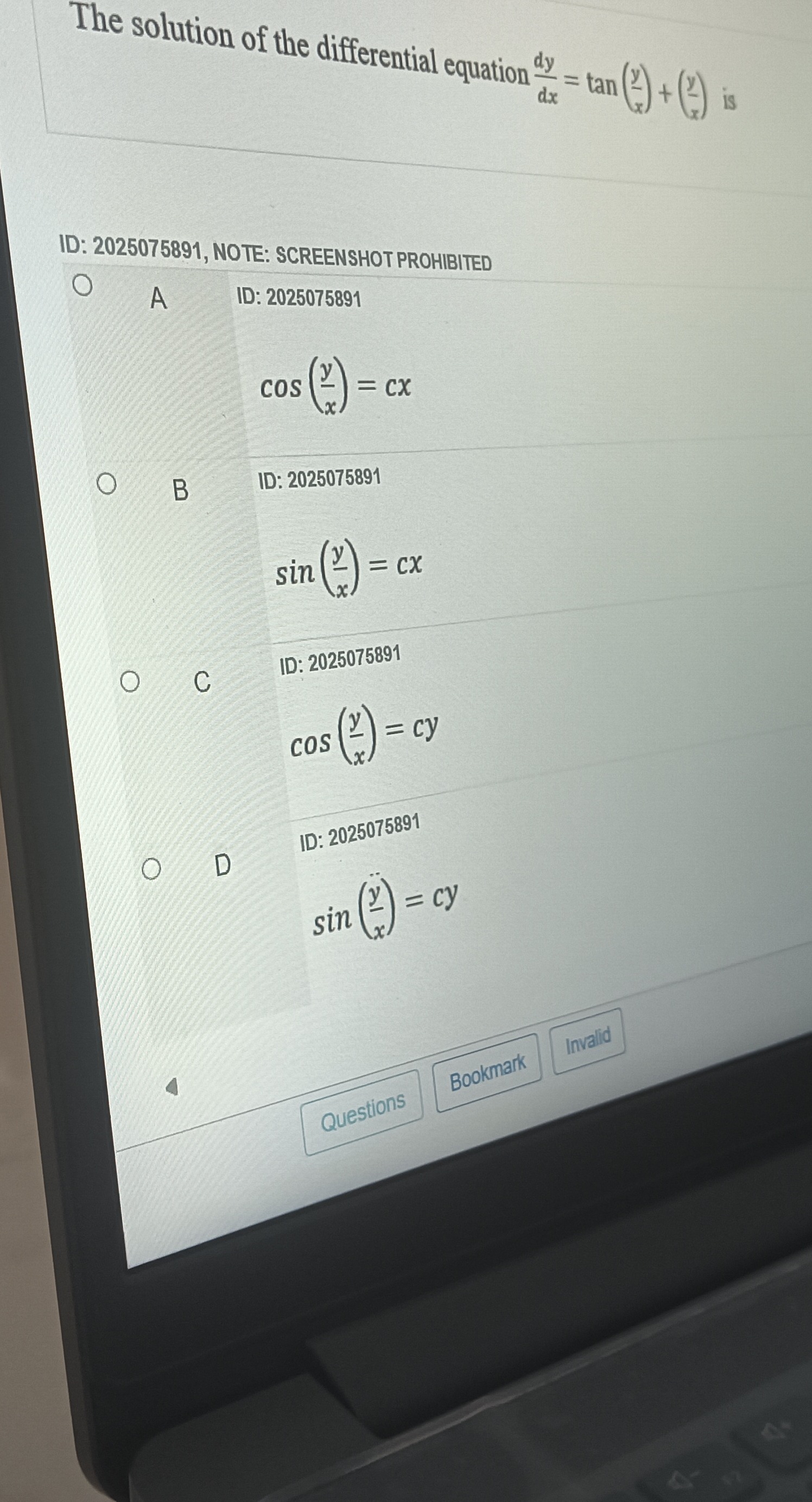
cos(xy)=cx
sin(xy)=cx
cos(xy)=cy
sin(xy)=cy
sin(xy)=cx
Solution
The given differential equation is: dxdy=tan(xy)+(xy)
This is a homogeneous differential equation because it can be expressed in the form dxdy=f(xy).
To solve homogeneous differential equations, we use the substitution y=vx. Differentiating both sides with respect to x, we get: dxdy=v+xdxdv
Substitute y=vx and dxdy=v+xdxdv into the original differential equation: v+xdxdv=tan(xvx)+(xvx) v+xdxdv=tan(v)+v
Subtract v from both sides: xdxdv=tan(v)
This is a separable differential equation. Separate the variables v and x: tan(v)dv=xdx cot(v)dv=xdx
Now, integrate both sides: ∫cot(v)dv=∫xdx
The integral of cot(v) is ln∣sin(v)∣, and the integral of x1 is ln∣x∣. We add a constant of integration, which can be written as ln∣C∣ for convenience: ln∣sin(v)∣=ln∣x∣+ln∣C∣
Using the logarithm property lna+lnb=ln(ab): ln∣sin(v)∣=ln∣Cx∣
Exponentiate both sides to remove the logarithm: ∣sin(v)∣=∣Cx∣
Since C is an arbitrary constant, it can absorb the signs, so we can write: sin(v)=Cx
Finally, substitute back v=xy: sin(xy)=Cx
