Question

The solubility of $Ca(CN)_2$ in 0.05 M NaCN solution is $x \times 10^{-6}$. The $K_{sp}$ of $Ca(CN)_2$ is $1.0 \times 10^{-8}$. Find the value x.

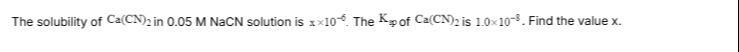
Answer 1

x = 4

Answer 2

For the dissolution of $\text{Ca(CN)}_2$:

$$\text{Ca(CN)}_2 (s) \rightarrow \text{Ca}^{2+} (aq) + 2\,\text{CN}^- (aq)$$

Let the solubility of $\text{Ca(CN)}_2$ be $s$ mol/L. Then:

$$[\text{Ca}^{2+}] = s \quad \text{and} \quad [\text{CN}^-] = 0.05 + 2s \approx 0.05 \quad (\text{since } 2s \ll 0.05)$$

The solubility product is:

$$K_{sp} = [\text{Ca}^{2+}][\text{CN}^-]^2 \approx s \times (0.05)^2$$ $$1.0 \times 10^{-8} = s \times 0.0025$$ $$s = \frac{1.0 \times 10^{-8}}{0.0025} = 4.0 \times 10^{-6}$$

Thus, $x = 4$.

In summary:

Assume solubility $s$. $[\text{CN}^-]$ is approximately 0.05 M. Set up $K_{sp} = s(0.05)^2$. Solve for $s$ to find $s = 4.0 \times 10^{-6}$, so $x = 4$.