Question

The smallest value of $k$, for which both the roots of the equation ${{x}^{2}}-8kx+16\left( {{k}^{2}}-k+1 \right)=0$ are real, distinct and have values at least $4$ is

Answer 1

For this problem we need to calculate the value of $k$ such that the given equation ${{x}^{2}}-8kx+16\left( {{k}^{2}}-k+1 \right)=0$ has real, distinct and have values at least $4$. Here we have the two considerations: the first one is the roots of the given equation are real, distinct and the second consideration is the roots have at least $4$. Now we will compare the given quadratic equation with the standard quadratic equation which is $a{{x}^{2}}+bx+c=0$ and write the values of $a$, $b$, $c$. If we observe that the concept related to nature of the roots depends on the discriminant of the quadratic equation, so we will calculate the discriminant value of the quadratic equation which is ${{b}^{2}}-4ac$. We need to have a positive discriminant to have real and distinct roots. From this we can obtain an expression and solve the expression to get the range of the $k$. Now we will consider the second part that the root has a value at least $4$. If the root has at least value of $4$, then the value of $f\left( 4 \right)$ should be greater than or equal to zero. From this also we can obtain an expression and solve for the range of $k$. After getting ranges of $k$, we can write the minimum value of $k$.

Complete step by step solution:
Given the equation, ${{x}^{2}}-8kx+16\left( {{k}^{2}}-k+1 \right)=0$.
Comparing the above given quadratic equation with the standard quadratic equation which is $a{{x}^{2}}+bx+c=0$, then the values of $a$, $b$, $c$ are
$a=1$, $b=-8k$, $c=16\left( {{k}^{2}}-k+1 \right)$.
The discriminant of the given quadratic equation will be
${{b}^{2}}-4ac={{\left( -8k \right)}^{2}}-4\left( 1 \right)\left[ 16\left( {{k}^{2}}-k+1 \right) \right]$
Simplifying the above equation by using the distribution law of multiplication and some other mathematical operations, then we will get
$\begin{aligned} & {{b}^{2}}-4ac=64{{k}^{2}}-64{{k}^{2}}+64k-64 \\\ & \Rightarrow {{b}^{2}}-4ac=64k-64 \\\ \end{aligned}$
If the given equation has a real, distinct roots then the discriminant of the given equation should be positive, we can write this mathematically as
${{b}^{2}}-4ac>0$
Substituting the discriminant value that we have calculated, in the above equation, then we will get
$64k-64>0$
Divide the whole expression with $64$ on both sides, then we will get
$k-1>0$
Simplify the above expression by adding $1$ on both sides, then we will have
$\therefore k>1.....\left( \text{i} \right)$
Now consider the point that the root has at least value of $4$. That means the given equation should give a positive or zero value when we substitute $4$ in the given equation. So, substituting $4$ in the given equation, then we will get
$f\left( 4 \right)={{\left( 4 \right)}^{2}}-8k\left( 4 \right)+16\left( {{k}^{2}}-k+1 \right)$
Simplifying the above equation by using mathematical operation, then we will have
$\begin{aligned} & f\left( 4 \right)=16-32k+16{{k}^{2}}-16k+16 \\\ & \Rightarrow f\left( 4 \right)=16{{k}^{2}}-48k+32 \\\ & \Rightarrow f\left( 4 \right)=16\left( {{k}^{2}}-3k+2 \right) \\\ \end{aligned}$
If the above value should be a positive or zero. It can be written as
$\begin{aligned} & f\left( 4 \right)\ge 0 \\\ & \Rightarrow 16\left( {{k}^{2}}-3k+2 \right)\ge 0 \\\ \end{aligned}$
Dividing the above equation with $16$ on both sides and splitting the middle term as $-3k=-k-2k$ and simplifying the expression by following some mathematical operations, then we will get
$\begin{aligned} & {{k}^{2}}-k-2k+2\ge 0 \\\ & \Rightarrow k\left( k-1 \right)-2\left( k-1 \right)\ge 0 \\\ & \Rightarrow \left( k-1 \right)\left( k-2 \right)\ge 0 \\\ & \Rightarrow k\ge 1\text{ or }k\ge 2......\left( \text{ii} \right) \\\ \end{aligned}$
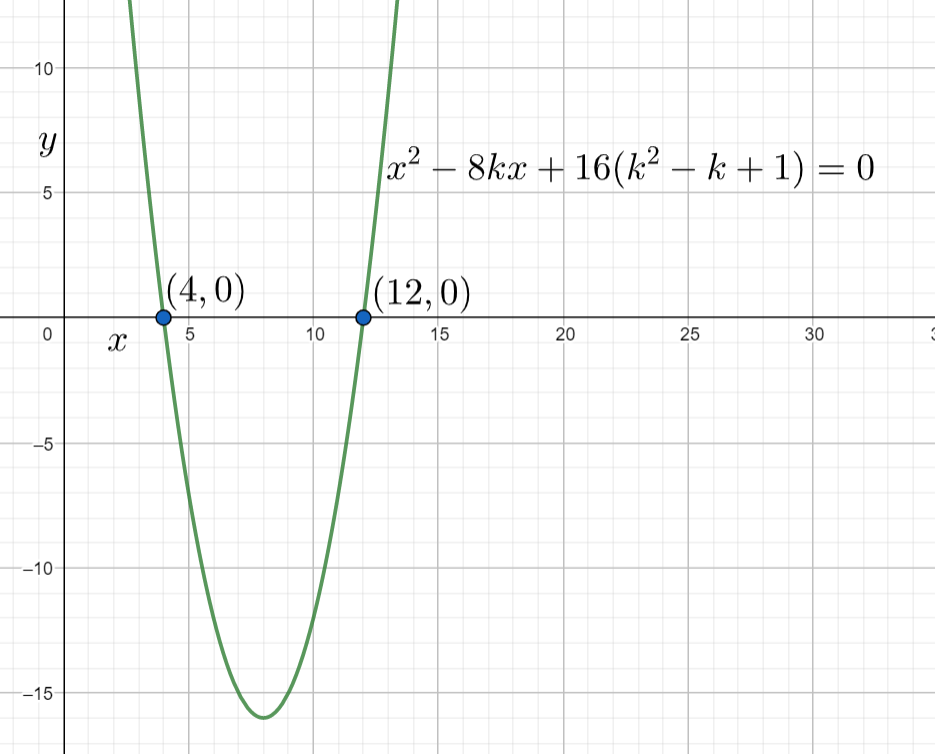
From equations $\left( \text{i} \right)$ and $\left( \text{ii} \right)$ we can say the minimum value of the $k$ is $2$.

Note: For this problem we can check for the value of $k$ by plotting the graph of the given equation for various $k$ values and observe whether the assumed $k$ values satisfy the given conditions or not. We can observe that for $k=2$ the given equation satisfies the given conditions and the graphs will look like below.